Узоры в полосе из геометрических фигур: Конспект интегрированной образовательной деятельности «Узор в полосе из чередующихся геометрических фигур»
Конспект интегрированной образовательной деятельности «Узор в полосе из чередующихся геометрических фигур»
Цель: способствовать закреплению знаний детей о геометрических фигурах.
Задачи:
1. Повторить названия и отличительные признаки геометрических фигур;
2. Развивать глазомер, внимание, кругозор, словарный запас;
3. Учить рисовать узор в полосе из геометрических фигур;
4. Воспитывать усидчивость, старание, аккуратность.
Интеграция областей: «Познание», «Художественное творчество», «Коммуникация».
Материалы: иллюстрации из геометрических фигур, наборы геометрических фигур, шаблоны, карточки с узорами, линейки, простые карандаши, акварельные краски, кисти.
Виды деятельности: коммуникативная, игровая, продуктивная.
Ход образовательной деятельности.
Организационный момент.
Нам вспомнить сегодня будет полезно,
Какие геометрические фигуры известны.
Слушаем сначала все внимательно загадки,
А потом берём и показываем отгадку.
Д/и «Отгадай и покажи»
• Что за фигура друзей и подруг
Собирает в большой и маленький?. (Круг)
• Три стороны и три угла,
И столько же вершин,
И трижды трудные дела
Мы трижды совершим. (Треугольник)
• Он давно знакомый мой,
Каждый угол в нём прямой,
Все четыре стороны
Одинаковой длины.
Вам его представить рад.
Как зовут его? (Квадрат)
• Четыре угла,
Четыре стороны,
Противоположные стороны равны. (Прямоугольник)
• Четыре угла,
Четыре стороны,
Стороны разной длины. (Трапеция)
— Скажите, чем отличаются друг от друга квадрат и прямоугольник? Пря-моугольник и треугольник?
Д/и «Найди отличия»
— Посмотрите, ребята, внимательно на две иллюстрации. Вот первая, а это вторая. Что изменилось на второй иллюстрации? Чем она отличается от первой? (Шапочка, туловище, руки, ноги, нос. )
)
— Что не изменилось? (Голова, глаза, рот.)
Д/и «Составь узор»
— Хорошо, дети! Теперь возьмите на столе возле себя геометрические фигуры и составьте из них узор как на образце. Будьте внимательны, следите за цветом. (Дети самостоятельно выполняют задание.)
— Посмотрите у своего соседа по парте, есть ли у него ошибки? Если есть, то объясните ему, где нужно исправить.
— Молодцы, очень красивые узоры у нас получились!
Беседа об орнаменте, его видах и назначении.
— Люди с давних времен украшали свою одежду, жилище, орудия труда и предметы быта различными орнаментами. На глиняных сосудах и на орудиях труда древних людей явственно различимы узоры: точки, прямые и волнистые линии, образующие орнамент, треугольники, кружочки в сочетании с линиями и растительными формами.
— Орнамент — это узор, построенный на ритмическом чередовании и сочетании геометрических фигур или элементов форм растительного и животного мира.
— Рассмотрите, ребята, внимательно эти три образца орнаментов. Скажите, под каким номером геометрический орнамент?
— Почему он так называется? (состоит из геометрических фигур)
— А сейчас найдите растительный орнамент.
— Почему он так называется? (состоит из листьев, ягод)
— Какой орнамент состоит из элементов растительного и животного мира? Назовите мне эти элементы.
Д/и «Какой орнамент». (Дети определяют вид орнамента — геометрический, растительный, животный или смешанный.)
— Основное назначение орнамента – украсить поверхность предмета. Орнамент встречается в нашей жизни везде. Очень красивы деревенские дома: ставни окон могут быть украшены орнаментом, который вырезали резчики. Он может быть очень красивым, например, из треугольников. Орнамент можно встретить у себя дома – на обоях, на дорожке, на посуде. Орнаментом и раньше украшалась не только одежда и полотенца, узор покрывал прялки, шкатулки, лавки и сундуки. Его даже можно его увидеть на печенье, которое все мы любим. Он может состоять из ромбиков, кружочков, квадратиков. То есть орнамент украшает нашу жизнь.
Он может состоять из ромбиков, кружочков, квадратиков. То есть орнамент украшает нашу жизнь.
— Вот и мы с вами сегодня будем учиться рисовать геометрический орнамент – узор в полосе из геометрических фигур, чтобы вы в будущем сами могли украсить любой свой предмет.
Физкультминутка.
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем два квадрата,
А на них огромный круг,
А потом ещё кружочек,
Треугольный колпачок.
Вот и вышел очень, очень
Развесёлый чудачок.
(Дети рисуют в воздухе пальцем геометрические фигуры.)
Объяснение построения рисунка по технологической карте.
— С помощью линейки и намеченных точек делим лист на три части. Проводим горизонтальные линии. Получили полосу.
— Также с помощью линейки и намеченных точек делим полосу пополам. Полученные половинки полосы делим ещё пополам.
— Помещаем в первое «окно» полосы квадрат, во второе – круг, обводим шаблоны. Аналогично с третьим и четвёртым «окошками». Не забываем про чередование.
— Сверху и снизу оформляем полосу каймой – узкой полоской.
— Оформляем узор из геометрических фигур в полосе указанными на образце цветами.
Самостоятельная работа.
— Начертите и раскрасьте узор в полосе согласно технологической карте и образцу. При раскрашивании не выходите за границу рисунка. Кому нужна помощь, поднимите руку.
Итог образовательной деятельности. Анализ рисунков.
— Узор получился яркий, геометрические фигуры правильной формы. Молодцы!
— Что мы сегодня рисовали?
— Что вам запомнилось и понравилось на занятии?
— Чем хочется поделиться с папой и мамой?
Конспект урока по ИЗО во 2 классе на тему » Рисование узора в полосе из чередующихся геометрических фигур».
Конспект урока ИЗО в специальной коррекционной
школе VIII вида (2 класс)
с использованием игровой технологии
Тема: « Рисование узора в полосе из чередующихся
геометрических фигур».
учитель ИЗО Соколовской школы-интерната
Попкова Е.В
Цель урока — учить детей украшать геометрическим узором формы.
Задачи урока:
1.Учить детей работать с трафаретом.
Приучение пальцев рук к точным, целенаправленным движениям, способствующие развитию и коррекции зрительно-двигательной координации.
2.Совершенствовать навыки раскрашивания рисунка, соблюдая контуры изображения при работе с акварельными красками.
3.Корригировать мыслительные процессы.
Оборудование урока: рисунки и иллюстрации по теме, образцы узоров,
трафареты прямоугольников разного размера, операционная карта, альбомы, простые карандаши, кисти, акварельные краски, баночки для воды.
Тип урока: комбинированный.
Ход урока.
Организационный момент. (1мин.)
Проверка готовности учащихся к уроку.
2. Беседа. (4 мин.)
(Объявляется тема урока).
Наша тема урока называется Рисование узора в полосе из чередующихся геометрических фигур
Сегодня мы будем с вами составлять узор в полосе. Посмотрите как она выглядит. На какую геометрическую фигуру она похожа. Правильно, прямоугольник. Как вы догадались? Сколько углов у прямоугольника? Ребята, вспомните, какие еще фигуры вы знаете? ( круг, квадрат, треугольник, овал). Покажите их на доске.
Возьмите в руки карандаши и все вместе мы сейчас попробуем их нарисовать их в воздухе. Послушайте стихотворение.
1) Быстро кружится пчела,
Ведь она нектар несла.
Делает она за кругом круг
И зовет своих подруг!
( Водим карандашом в воздухе рисуя круги)
2) Муравей домой спешил
И соломинку тащил.
Братцы строят новый дом,
Будут жить зимою в нем!
( покажите как выглядит домик у муравья. Начинаем с основания домика. Рисуем прямоугольник, над ним рисуем квадрат, затем крыша. На какую фигуру она похожа? треугольник).
У вас на партах лежат трафареты прямоугольника. Посмотрите внимательно сколько их и какого они размера? (три, от большего к меньшему)
3. Объяснение. (Работа с операционной картой).(9-11 мин.)
Учитель демонстрирует этапы работы, а учащиеся за ним выполняют.
1) Расположите большой прямоугольник в центре альбомного листа и обведите его. Молодцы! Правильно.
2) Внутри большого прямоугольника обведите прямоугольник меньшего размера.
3) Обведите последний прямоугольник самого маленького размера.
4) Половина нашего рисунка готово. Теперь нам необходимо раскрасить узор в прямоугольнике. Посмотрите какие узоры могут быть выбраны.
( демонстрация узоров для треугольников). Цветочки, кружочки, сеточка, полосочки. Какого они цвета? …
4. Самостоятельная работа учащихся.(15-16мин.) (музыка)
А теперь самостоятельно расписываем узор.
(Фронтальная и индивидуальная помощь учащимся со стороны учителя).
В процессе раскрашивания учащиеся вспоминают о способности смешивания красок.
Учитель задает вопрос учащимся.
5) . Отложили в сторону карандаши, давайте не много с вами отдохнем.
5. Физ. минутка.(2 мин.)
Под весенние напевы
Повернемся вправо, влево.
Руки вверх, руки вниз.
Вправо, влево головою,
Руки вверх, перед собою.
Топнем правою ногою,
Топнем левою ногою
И покрутим головою.
Голову поднимем выше
И легко подышим.
6. Выставка работ учащихся. Выставление оценок (4-5 мин.)
На доске выставляются все работы учащихся, проводится анализ их выполнения и выставление отметки (отметка ставится коллективно – учителем и учениками).
7. Подведение итогов.(2-3 мин.)
Учитель задает вопросы учащимся.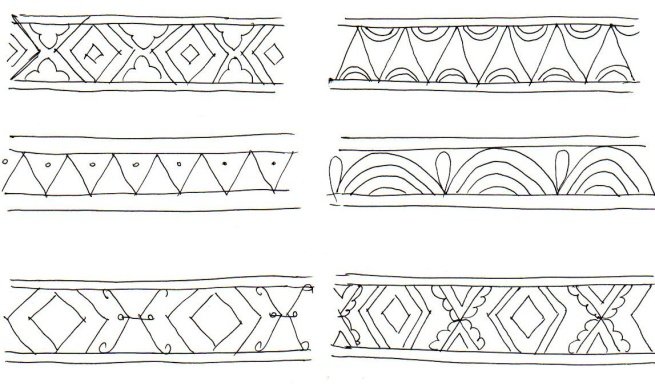
― Какая была тема сегодняшнего урока?
― Что мы рисовали?
― На какой предмет похож прямоугольник? (кирпич)
― Что мы нарисовали в прямоугольнике? (узор)
― Какую форму имеют узоры в прямоугольнике? ( цветочки, сеточка, круги…)
Все молодцы. Хорошо нарисовали. На этом наш урок закончен.
Дежурные убирают рабочие места.
Рисование простейших узоров в полосе
Аннотация
Дидактическая модель урока оформлена в виде методического пособия для подготовки и проведения урока изобразительного искусства в 1 классе. Урок разработан по технологии коррекционно-развивающего обучения и направлен на развитие психических механизмов, лежащих в основе способности учащихся. Игровая форма обучения сочетается с использованием информационных технологий, что способствует повышению мыслительной активности учащихся. Наглядное представление учебного материала выполнено в виде слайдов.
Тема
«Декоративное рисование.
Рисование в полосе узора из растительных форм».
Цель урока:
-Формировать и развивать умения видеть и передавать в рисунке характерные особенности растительных фор;
-учить детей чередовать элементы при составлении в полосе узора.
Коррекционные цели:
Коррекция познавательной деятельности на основе упражнений: сравнения, развитие творческого воображения, процесса анализа и синтеза, коррекция цветового восприятия.
Воспитательные цели:
Формирование личности учащихся, воспитание любви к природе
Ход урока
Организационный момент.
а) Упражнение по развитию внимания: уберите лишний предмет.
— форма;
— размер;
— цвет. Слайд 1—з
б) актуализация опорных знаний: исправьте ошибку (в геометрическом узоре нет чередования). Слайд 4
-Как правильно? Что получилось? Какой узор (орнамент)? Какие геометрические фигуры использовались? А какие вы еще знаете геометрические фигуры?
Введение в тему урока.
— Ребята, скажите, а зачем нужны узоры?
( узорами украшают предметы: посуду, одежду и т.д.)
— Правильно. Вещи, которыми мы пользуемся, должны приносить не только пользу, но и быть эстетически оформленными, т.е. быть красивыми. Издавна люди стремились украшать вещи, которые окружали их. Давайте отправимся с вами в прошлое и посмотрим, какие узоры, орнаменты умели рисовать и вышивать наши бабушки, прабабушки.
Слайд 5-12
— Посмотрите, и сейчас, в наше время люди украшают предметы быта.
(учитель демонстрирует предметы быта, украшенные различными узорами)
— Ребята, давайте рассмотрим узоры, которые изображены на экране. Из каких фигур выполнены эти узоры.
(геометрические фигуры, цветы, листочки, животные)
— Правильно. Вы видите, что узоры не всегда могут быть составлены только из геометрических фигур. Если в рисунок узора входят листики, цветы, веточки, то такой узор называется растительным. Как вы думаете, почему? (ответы детей)
Слайд 13
И сегодня мы с вами на уроке будем учиться составлять, а затем рисовать растительный в полосе растительный узор.
3. Изучение нового материала.
— Скажите, из чего состоит растительный узор?
— А где можно найти сразу и цветы, и грибы, и листочки для нашего узора?
(в лесу)
— Я предлагаю вам отправиться в лес и собрать предметы для нашего узора. А что мы возьмем с собой, что бы принести это все из леса? (корзинку)
На доску вывешивается рисунок корзинки, учитель по ходу урок вставляет картинки в неё.
Слайд 14-21
(На экране изображение природы. Музыкальное сопровождение)
— Ой, ребята, тише, посмотрите, кто-то там притаился за кустом.
Это что за зверь лесной?
Встал, как столбик под сосной.
И стоит среди травы –
Уши больше головы. Слайд 22
(заяц)
— Ребята, посмотрите, какой красивый гриб растет на полянке. Давайте попросим зайчика сорвать нам грибок для нашего узора.
(Но около грибочка летает мотылек и просит ребят не срывать грибок, так как он там живет)
Слайд 23
— Ну что же ребята, не будем срывать домик у мотылька. А зайчик принес нам в подарок цветок и ягодку. (учитель вывешивает в корзинку рисунки ягоды и цветочка).
Слайд 24
— Заяц посоветовал нам отправиться за грибочком к его знакомой. Кто она?
В дупле на старом дубе
Живу в густом лесу.
Хожу в пушистой шубе,
Орешки я грызу. (белка) Слайд 25
— Ребята, посмотрите, что делает белка? (сушит грибы)
— Зачем она это делает? (заготавливает себе еду на зиму)
— Попросим у белочки грибок для нашего узора. Но белочка предлагает ребятам решить задача.(белка задает задачу, дети отвечают)
Но белочка предлагает ребятам решить задача.(белка задает задачу, дети отвечают)
Слайд 26
Белочка дает гриб, учитель вывешивает рисунок в корзинку.
Слайд 27
— Что это там в траве шуршит?
(Звуковое сопровождение — шорох.)
Сердитый недотрога
Живет в глуши лесной.
Иголок очень много,
А нитки ни одной. (ежик) Слайд 28
— Ребята, что делает ежик?
(носит листья к себе в норку, он готовится к зиме, теплее ему будет спать)
— Давайте попросим листик у ежика для нашего узора:
Ежик, ёжик подожди
Листик ты нам подари.
— Какие листочки дарит нам ежик?
(кленовый, дубовый) Слайд 29
— А это листок, какого дерева?
(детям незнаком лист, затрудняются в ответах)
Учитель рассказывает, что это лист рябины, показывает картинку, на экране изображение дерева рябины.
Слайд 30
Учитель прикрепляет листики на доску к корзинке.
— Вот корзинка наша полна, пора возвращаться. Попрощаемся с лесом.
4. Физминутка.
Шли мы лесом,
Шли мы полем.
Нас деревья провожали,
Дружно ветками махали.
Ветерок нас обдувал,
К речке быстро мы спустились,
Наклонились и умылись.
Вышли на берег крутой
И отправились домой.
5. Практическая работа. Составление узора в полосе.
Составление узора в полосе.
— Ребята давайте вспомним, как правильно построить полоску для узора.
(по опорным точкам, с помощью трафарета)
— Правильно. Посмотрите, как я буду строить полоску на доске. (Выполняет рисунок на доске с подробным комментированием)
— А теперь посмотрите на экран. (На экране выполняется последовательное построение полосы по опорным точкам)
Слайд 31
6. Разминка для кистей и пальцев рук
— Для того чтобы начать работу в альбомах, давайте подготовим наши пальчики.
— Вы были сегодня в лесу. Покажите мне как спят цветы. А вот солнышко пригрело и цветы распускаются. Прилетели бабочки садятся на цветы. Давайте мы раскрасим цветы и бабочки. (анимационные изображения предметов на экране с музыкальным сопровождением).
Слайд 32
7. Работа в альбомах.
Учитель предлагает детям нарисовать полоску в альбомах и разделить её. (дети выполняют работы по опорным точка или по трафаретной метке)
8. Работа по составлению узора.
Для составления узора учитель с детьми выбирает предметы из корзины. За основу узора берут грибок и дубовый лист. Разбирается порядок и варианты составления узора. Просматривается правила выполнения узора на экране.
Слайд 33
У детей на парте лежит раздаточный материал. Учитель предлагает взять грибок и листик и составить разные варианты узора.
Дети составляют узор, а затем выполняют его в альбомах. (обводка предметов по контуру)
9. Работа по раскрашиванию узора.
Учитель предлагает вспомнить ребятам, как нужно правильно красить предмет. Предмет разбивается на части (ножка, шляпка), выбирается цвет для каждой части. Учитель показывает на доске как правильно штриховать гриб. Затем показ штриховки шляпки гриба на экране. Аналогично проводится работа по раскрашиванию листочка.
Предмет разбивается на части (ножка, шляпка), выбирается цвет для каждой части. Учитель показывает на доске как правильно штриховать гриб. Затем показ штриховки шляпки гриба на экране. Аналогично проводится работа по раскрашиванию листочка.
Слайд 34-35
10. Самостоятельная работа учащихся.
(работа выполняется под музыкальное сопровождение)
Слайд 36
11 Выставка выполненных работ учащихся.
Учитель вывешивает готовые работы на доску.
12. Закрепление пройденного материала.
— Учитель у нас в корзинке остались ягоды и цветы. Покажите какой узор можно сложить из этих растительных форм. Сложите узоры у себя на парте. (один ученик выходит к доске и украшает узором вырезанный из бумаги кувшин.)
12. Подведение итогов урока.
1. Организационный момент. Привлечь учеников к активной деятельности. 2. Настрой на урок Способствовать преодолению снятия эмоционального напряжения. 3. Изучение нового материала. Показать неразрывную связь искусств. 4.Физминутка. сменить вид деятельности и привести мышцы в тонус. 5.Практическая часть. 6.Итог урока подвести итог, оценить результат деятельностиобучающихся на уроке. 7. Домашнее задание | Приветствие учащихся, эмоциональный настрой коллектива, проверка степени готовности к уроку. -Скажите, ребята, какой у нас сейчас урок? -Какой, по счёту? -Посмотрите на доску, что вы видите? -Что изображено на посуде, на мебели? -Кто мне ответит, как называются эти рисунки? Узор – орнамент — Это украшение, которое состоит из рисунков, они повторяются и чередуются между собой через определенные расстояния. -Как вы считаете, для чего нужен узор? -Какие бывают узоры? —Как же нам понять какой перед нами орнамент?(растительный или геометрический) -Скажите, из каких элементов можно составить растительный узор (орнамент)? -Из каких элементов можно собрать геометрический узор (орнамент)? Узор можно располагать в круге, в квадрате, в полосе. Узорами украшают посуду, одежду и многое другое. Например, платки и косынки, сумки, стены и окна домов. Художник, прежде чем начнет изображать узор, придумывает композицию, и только потом эту схему заполняет конкретными элементами. Композиция-это красивое сочетания различных предметов в определённом пространстве. -На партах у каждого из вас лежит конверт, откройте его. Из предложенных картинок, вам необходимо составить два вида узора. Проверка. Сегодня на уроке мы, будем учиться рисовать узор из геометрических фигур в полосе. -Сейчас ребята посмотрите на узор. -Скажите, к какому виду орнамента относится, этот узор? -Скажите, в какой геометрической фигуре нарисован данный узор? А точнее это широкая полоса, в которой нарисованы геометрические фигуры. -Какие фигуры? -Какими цветами раскрашен узор? Такой узор в полосе называется БОРДЮР, он может чередоваться и быть очень длинным. -Что можно украсить таким узором (бордюром)? Сейчас посмотрите на доску, я покажу вам последовательность выполнения этого узора. Отступив от верхнего края альбомного листа, проводится, прямая горизонтальная линия от левого края к правому краю листа. У вас в альбоме уже отмечены две опорные точки, от которых вы проведёте две прямые линии до правого края листа. В итоге получится широкая полоса (бордюр) в которой будем рисовать треугольники. На парте у каждого из вас лежит по одному шаблону треугольника, воспользуемся ими. Возьмите шаблон, от левого края плотно прижав, обведите. По верхнему и нижнему краю узора проводим обводку, в которой с верху вниз прямыми наклонными линиями рисуем зигзаг. После построения можно приступать к закрашиванию элементов узора. Обратите внимание на то что треугольники раскрашены по разному, чаще смотрите на представленный образец. Но прежде давайте с вами все встанем из за парт и маленько разомнемся. Целью вашего практического задания будет являться составление узора в полосе с использованием геометрических элементов и с последующим цветовым решением. Давайте еще раз повторим с вами основные ключевые моменты выполнения узора в полосе: ваш лист бумаги должен иметь форму полосы, поэтому он будет лежать горизонтально, параллельно парте. Далее следует инструктаж последовательности работы над рисунком. — Но прежде чем, приступить к практической работе, нам необходимо повторить Правило рисования: — перед тем как преступить к рисованию, необходимо правильно сесть: спину держать прямо, не наклоняться в какую-нибудь сторону, кисть не должна быть напряжена и не должна висеть в воздухе. Как правильно делать штрихи и (мазки): они должны располагаться друг возле друга, без каких-либо пропусков, не должны выходить за контур рисунка. -А теперь приступайте к практической работе. -Желаю вам творческой удачи! При затруднении более слабым ученикам оказывается помощь. Перед тем как дети приступят к рисованию, обратить их внимание на то, что необходимо соблюдать цветовое решение. Во время самостоятельной работы следить за осанкой учащихся. Учитель наблюдает за работой детей, помогает при возникновении трудностей. Устраивается просмотр (дети раскладывают свои работы на парте, проводится анализ рисунков, выбираются лучшие работы, обсуждаются, выставляются оценки). Продумать композицию растительного узора в любой геометрической фигуре (круг, квадрат, треугольник). | Настраиваются на урок. Урок рисования. Пятый. Ответы учеников. (Различные предметы: посуда, мебель) Рисунки. Узоры. Ответы учеников. Чтобы украшать им вещи. Так они становятся красивее. Ответы учеников. (растительные и геометрические) Ответы учеников. (листья, цветы, травка, ягода и.т.д). (из всех геометрических фигур, точек и линий). Учащиеся составляют узоры. (растительный и геометрический) Определения вида орнамента. (геометрическому) Ответы учеников. Прямоугольник. Ответы учеников. (треугольники, синий, зелёный, оранжевый) Ответы учеников. (края посуды, одежды, обои и т.д.) Ученики смотрят и слушают объяснения учителя. Выполняют упражнения Обучающиеся, повторяют правило рисования. Рисуют. Запись в дневник. |
Презентация на тему: Вырезание различных геометрических фигур, составление из них узоров в полосе
1
Первый слайд презентации: Вырезание различных геометрических фигур, составление из них узоров в полосе
Изображение слайда
2
Слайд 2
Правила работы на уроке ручного труда
Внимательно слушай объяснение учителя.
Не бери инструменты во время объяснения
учителя.
3. Приступай к заданию только после
объяснения учителя.
4. Приступай к работе медленно, не торопясь.
Не мешай работать тому, кто сидит рядом.
Если работа не получается – не волнуйся,
обратись за помощью к учителю.
Изображение слайда
3
Слайд 3
Правила безопасности при работе с ножницами :
держать острыми концами только вниз ;
— оставлять на столе с закрытыми лезвиями;
— передавать закрытыми кольцами вперед;
— не бросать с раскрытыми лезвиями;
— пальцы левой руки держать в стороне от лезвия;
Изображение слайда
4
Слайд 4
Техника безопасности при работе с клеем:
— запрещается брать клей в рот, мазать им волосы, одежду;
— нельзя, чтобы клей попадал на пальцы рук, лицо, особенно глаза;
— при попадании клея в глаза надо немедленно промыть их большим количеством воды;
— по окончании работы обязательно вымыть руки.
Изображение слайда
5
Слайд 5
Словарная работа.
Аппликация – это способ наклеивания на бумагу разноцветных кусочков бумаги для создания различных изображений, орнаментов.
Орнамент означает « украшение», узор, в котором сочетаются и повторяются геометрические фигуры и изобразительные элементы.
Изображение слайда
6
Слайд 6
Изображение слайда
Изображение для работы со слайдом
7
Слайд 7
Изображение слайда
Изображение для работы со слайдом
8
Слайд 8
Изображение слайда
Изображение для работы со слайдом
9
Слайд 9
Изображение слайда
Изображение для работы со слайдом
10
Слайд 10
План
Подготовка рабочего места.
Выбор поделки.
Подготовка и изготовление нужных фигур.
Сборка аппликации.
Наклейка деталей.
Изображение слайда
11
Слайд 11
Спасибо за урок!!!
Изображение слайда
Изображение для работы со слайдом
12
Последний слайд презентации: Вырезание различных геометрических фигур, составление из них узоров в полосе
Изображение слайда
Паркетри, использование симметричных кусков шпона для создания орнаментов
В паркетри используются симметричные куски шпона, которые образуют геометрические орнаменты. Формы узоров взяты из начальной геометрии. Можно выполнить любые орнаменты посредством объединения вырезанных кусочков шпонов различного цвета, текстуры или типа в форме квадратов, прямоугольников, треугольников, ромбов или других многоугольников.
Составление орнамента паркетри
Перестановка простых геометрических фигур позволяет составлять огромное количество разнообразных орнаментов. Можно поэкспериментировать с составлением узоров на бумаге с квадратной или изометрической сеткой, закрашивая с помощью разноцветных карандашей или ручек элементы вашего орнамента (1). Узоры с повторяющимися полосами легче размечать, вырезать и набирать. Узоры с переплетающимися элементами, как, например, кубы или звезды, набираются индивидуально.
Можно поэкспериментировать с составлением узоров на бумаге с квадратной или изометрической сеткой, закрашивая с помощью разноцветных карандашей или ручек элементы вашего орнамента (1). Узоры с повторяющимися полосами легче размечать, вырезать и набирать. Узоры с переплетающимися элементами, как, например, кубы или звезды, набираются индивидуально.
Подготовка к работе
Как и при любых цикличных операциях, простейший шаблон поможет работать точно и последовательно. Сделайте шаблон из куска искусственной панели в форме квадрата со стороной 600 мм. К поверхности панели вровень с одной из кромок укрепите шурупами металлический или деревянный упор примерно 6-миллиметровой толщины. Проведите две базовые линии под углом 90° к упору (2) и любые другое базовые линии под необходимыми углами для данного проекта.
Резка производится ножом или пилкой для шпона с помощью поверочной линейки в качестве направляющей. Для установки линейки параллельно упору вырежьте пары фанерных ограничителей нужных размеров. Потребуется также клейкая лента для фиксации элементов.
Орнамент «шахматная доска»
Самым, возможно, известным примером геометрического орнамента паркетри является узор «шахматная доска», где стоящие рядом одинаковые по размеру квадраты имеют разный цвет. Разницу в цвете можно получить, применяя шпоны контрастирующих цветов или, для более тонкого эффекта, один и тот же шпон, но с разным направлением волокон в соседних квадратах. В целом наилучший эффект получается при использовании шпона с прямыми или слабо выраженными волокнами.
Выберите листы шпона и нарежьте из них полосы немного длиннее предполагаемой основы. Ровно обрежьте одну кромку у каждой полосы. Прижмите этой кромкой полосы к упору и обрежьте их по требуемой ширине с помощью пары фанерных ограничителей для правильной установки поверочной линейки (1). Сделайте четыре полосы одного цвета и пять другого — без привязки цвета к количеству. Это для того, чтобы сохранять направление волокон в наборе. Пронумеруйте их в соответствии с порядком вырезания. Аккуратно состыкуйте полосы, перемежая цвета, и склейте их вместе лентой. Положите набор на доску (шаблон) для резки, выровняв одну боковую кромку по перпендикулярной базовой линии. С помощью малых мерных ограничителей установите поверочную линейку параллельно упору и ровно обрежьте концы полос (2). Удалите отход и подвиньте обрезанные торцы к упору. Разрезав набор на полосы тем же способом, получите полосы, состоящие из квадратов с чередующимися цветами.
Пронумеруйте их в соответствии с порядком вырезания. Аккуратно состыкуйте полосы, перемежая цвета, и склейте их вместе лентой. Положите набор на доску (шаблон) для резки, выровняв одну боковую кромку по перпендикулярной базовой линии. С помощью малых мерных ограничителей установите поверочную линейку параллельно упору и ровно обрежьте концы полос (2). Удалите отход и подвиньте обрезанные торцы к упору. Разрезав набор на полосы тем же способом, получите полосы, состоящие из квадратов с чередующимися цветами.
Опять склейте отрезанные кромки, но сдвинув соседние полосы на один квадрат (3). Отрежьте выступающие квадраты, чтобы получилась ровная шахматная доска. Вырежьте обрамления, приклейте их лентой по периметру — и набор готов к обработке прессом.
Варианты полос
С помощью способа выкладывания орнамента «шахматная доска» можно создавать целый ряд различных узоров. Вырезая полосы разной ширины и смещая полосы на половину или на целый цветовой элемент, можно получать массу вариантов.
Если квадраты разрезать по диагонали, получатся полосы с прямоугольными треугольниками, которые при смещении наполовину дают зигзагообразный рисунок. Если соседние полосы перевернуть и сдвинуть, получатся треугольники с чередующимися цветами. Ромбические узоры выполняются резкой полос под углом 60°. Сначала вырежьте параллельные полосы из контрастирующих шпонов заданной ширины. Укрепите кнопками первую полосу вровень с базовой линией заранее прочерченной на шаблоне под углом 60°. Затем приклейте полосы друг к другу лентой так, чтобы углы концов касались упора. Обрежьте «зубцы» концов с помощью поверочной линейки и мерных ограничителей. Удалите кнопки и придвиньте обрезанную кромку к упору.
Еще раз разрежьте набор на полосы, используя те же ограничители. Теперь получились полосы из ромбов с углом 60°, которые, если их сместить на один ромб и склеить вместе лентой, образуют повторяющийся узор из чередующихся элементов.
При разрезании этого набора горизонтально через центры ромбов получаются полосы равносторонних треугольников. Их также можно переворачивать и смещать для составления различных орнаментов.
Их также можно переворачивать и смещать для составления различных орнаментов.
Кубический узор
Классический эффект изометрического (объемного) куба достигается вырезанием ромбов с углом 60° из древесины трех разных оттенков и соединения ромбов в шестиугольник.
Для того чтобы сделать симметричный повторяющийся узор, сначала вырежьте ромбы, используя метод полос, но склеивайте их лентой менее прочно. Разделите ромбы и наберите поле из шестиугольников на прозрачной клеящей пленке, положенной на ваш трафарет с изометрической разметочной сеткой липкой стороной вверх.
Покройте набор гуммированной (клеевой) бумагой и поместите между двумя ровными панелями. После высыхания удалите пленку, чтобы подготовить набранный узор к укладке.
Математика вокруг нас. Узоры и орнаменты на посуде
1. ПРОЕКТ
По предмету: «Математика 2 класс»
На тему: « Математика вокруг нас.
Узоры и орнаменты на посуде»
выполнил: ученик 2 класса
Д.Ж.Ямгуров
2. Цели:
Выяснить формы
элементов
применяемых
для
декора
посуды;
Геометрические фигуры;
Виды художественной росписи.
Техника росписи
посуды и
особенности орнамента определялись
местностью
и
обычаями
проживавших на ней людей.
Орнаменты — это узоры состоящие
из линий, кругов, соединенных и
повторяющихся.
Основными
геометрическими
фигурами
на
плоскости являются точка и прямая линия.
Отрезок, луч, ломаная линия — самые простые
геометрические фигуры на плоскости.
Среди геометрических
линий следует выделить:
прямые; ломаные;
волнообразные; точечные.
Точечная роспись — множество мелких точек
из которых образуется орнамент на тарелке.
Геометрический стиль росписи посуды появился 8 вв. до н.
э.; горизонтальные полосы, линейные узоры и геометрических
фигур, четко показывали форму посуды;
изогнутая
непрерывная
линия,
образующая
окантовку большинства узоров элементы
Разновидности и мотивы узоров.
Орнаменты народов мира
включают такие мотивы:
пересечение линий в
горизонтальном и
вертикальном порядке;
совмещение одинаковых
окружности, построенные
на геометрии фигур.
Хохлома. Дешевую обиходную
посуду можно было отличить по
простым узорам Это спирали,
ромбики, мелкие розетки и
листики.
Пряник — чаще всего
встречается внутри чаш или
блюд, и представляет собой
геометрическую фигуру в
виде ромба или квадрата,
украшенную
ягодами,
цветами, травой.
Гжель — художественная
роспись с
нанесением
растительных
и
геометрических
орнаментов
, с
использованием точек и линий.
Гжельская продукция: посуда, часы, камины,
люстры и многое другое является
неотъемлемой частью нашей жизни.
Бордюр- совокупность равных фигур,
повторяющихся одна за другой вдоль
прямой линии.
Симметрия на
плоскости
относительно прямой
линии называется
осевой симметрией, а
также отражением от
прямой, является как
бы зеркальным
отражением.
Вывод:
Изучив данный материал можно сделать вывод что
геометрия важный раздел математики. Ее возникновение
уходит в глубь тысячелетий и связано прежде всего с
развитием ремесел, культуры, искусства.
Художнику математика необходима для его искусства.
Учение о геометрии является предметом искусства, без
нее ничего в живописи создать невозможно.
В наше время изделия из хохломы и гжели из
повседневных
превратились
в
декоративные
и
появляются в виде декора . Это прекрасные сувениры,
которые можно подарить к любому празднику..
Полоски с рисунком
Полоски узора позволяют использовать выбранные вами изображения в узоре. Например, если вы выбрали яблоко, банан и другие различные фрукты, первым узором будет узор AB: яблоко, банан, яблоко, банан и т. Д. Есть три ряда начала разных узоров.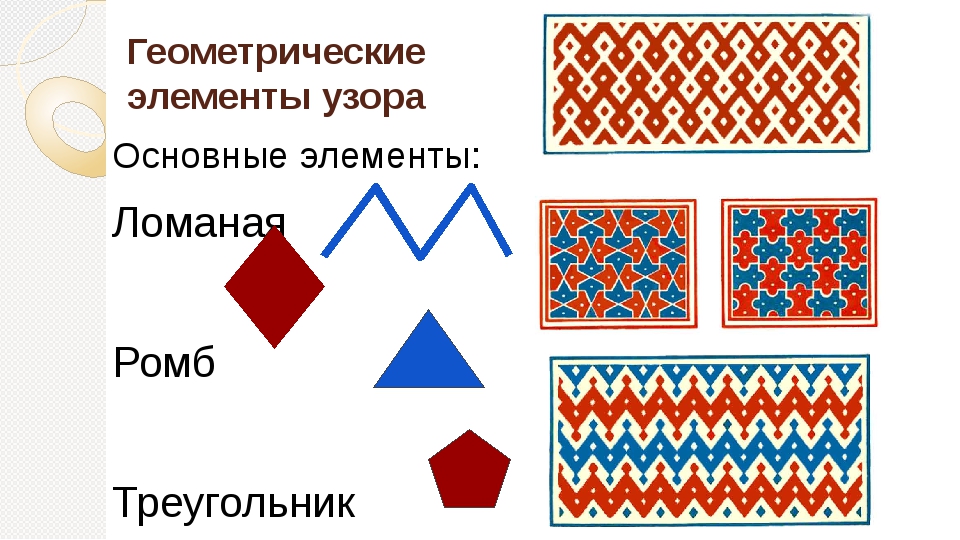 За выкройками следуют прямоугольники, чтобы ученик мог завершить оставшуюся часть выкройки. Дополнительные картинки для заполнения узора находятся внизу страницы.
За выкройками следуют прямоугольники, чтобы ученик мог завершить оставшуюся часть выкройки. Дополнительные картинки для заполнения узора находятся внизу страницы.
(образец полоски с образцом словарного запаса Хэллоуина)
Создание материалов:
При создании материалов учитель может выбирать картинки по теме или концепции.Логопед может выбрать картинки с определенными фонемами или многосложными словами для практики артикуляции. Полоски можно разрезать по рядам вместе с маленькими картинками и ламинировать.
(образец полосы шаблона минимальных пар TH и F)
Для прикрепления изображений:
- Velcro- Маленькие картинки можно прикрепить на липучке, чтобы дети продолжили узор в коробках.
- Магниты- Положите полоски с рисунком на противень.Прикрепите магнит к обратной стороне маленьких картинок, используемых для продолжения рисунка. Попросите учащихся разместить магнитные картинки, чтобы продолжить узор. (Отлично сочетается с пряниками или едой).
- Клей-карандаш — В небольшой группе раздайте каждому ребенку полоску с выкройками и поместите маленькие картинки в центр стола. Попросите учащихся определить, какие картинки им нужны для продолжения их рисунка.
Использование в классе:
Полная группа: Используйте липучку, чтобы создавать материалы многоразового использования и составлять диаграммы классов с полосками выкройки.Во время полных групповых уроков попросите учащихся выполнить выкройку. Это может быть хорошим введением перед тем, как учащиеся начнут работать самостоятельно или со сверстниками.
Малая группа: Разместите полоски с выкройками в центре стола, чтобы учащиеся могли заполнить их во время работы в малых группах.
Центр: Поместите полоски выкройки в соответствии с темой или единицей обучения в корзину в математическом центре.
Рабочий стол: Поместите выкройки на один из столов по прибытии.Когда учащиеся входят в класс, они могут выбирать полоски с выкройками в качестве одного из занятий, которые они могут выбрать, ожидая прибытия сверстников, распаковки и подготовки к началу дня.
Использование с манипуляторами / объектами: Вы можете создавать узоры с цветными формами и предлагать учащимся использовать различные манипуляции с цветными полосками узоров. Например, используйте квадраты и попросите учащихся использовать цветные блоки, используйте круги и попросите учащихся использовать цветные деревянные бусины для создания узора или использовать различные формы и попросить учащихся использовать блоки для узоров.Кроме того, учителя могут создавать полоски с рисунками, которые соответствуют маленьким манипуляторам или предметам в классе. Например, используйте цветных медведей или маленькие машинки. Создавая коллекцию изображений для полос с узорами, вы часто можете изменить цвет (или стиль — на черно-белый, чтобы раскрасить себя) каждого изображения в библиотеке LessonPix.
Одноклассник: Соедините ученика с полными наборами полосок для выкройки. Поощряйте пару произносить каждый узор вслух, работая вместе над его завершением.
Дифференцированное обучение: Учителя могут дифференцировать обучение, используя более простые схемы для некоторых учеников и более сложные схемы для учеников более высокого уровня. Это позволяет учителю выстраивать урок по построению паттернов в соответствии с индивидуальными уровнями обучения.
Смарт-доска / Интерактивная доска: Перед началом урока создайте урок по программному обеспечению для записной книжки с такими же рисунками и рисунками. В коллекции вы можете щелкнуть отдельные изображения, используемые для создания полосы рисунка, и перетащить их в программу для ноутбука или в текстовый документ.Создайте начало того же рисунка и оставьте дополнительные картинки внизу страницы, чтобы дети могли перетащить их, чтобы завершить свой рисунок.
Во время урока раздайте полоски с выкройками ученикам в небольшой группе, когда они сядут у доски. Посмотрите на выкройку и попросите учеников заполнить полоску выкройки. Затем попросите одного из учеников показать на доске, как составлять узор. Это укрепит изучение шаблона и словарного запаса, не только выясняя его сами по себе, но и произнося это вслух вместе.
Бесплатный образец полосок с узором осенних листьев
Энциклопедия тканевых и текстильных узоров
Узоры — это повторение элемента или мотива, используемого для создания уникального украшения на ткани. Примером легко узнаваемого узора является узор в клетку или полосатый узор. Но доступны сотни различных шаблонов, и каждый из них обозначен ярлыками (именами), чтобы помочь в описании и выборе продукта.Ниже приведен исчерпывающий словарь типов узоров, используемых в дизайне тканей, текстиля и одежды.
Геометрические узоры
Все узоры можно разделить на геометрические или органические. Геометрические узоры могут быть далее разделены на абстрактные узоры, узоры (повторяющиеся формы и размеры, не имеющие отношения к природным объектам. Примеры геометрических узоров включают геометрические формы и пледы.
Органические (узоры, вдохновленные природой)
Есть два типа органических узоров.Реалистичные узоры — это повторения природных объектов, а стилизованные — более простые повторения природных объектов.
В категориях геометрических и органических узоров есть десятки конкретных типов узоров. Некоторые узоры могут пересекать линии и относиться к нескольким типам узоров.
Ниже представлены многие типы выкройки ткани.
Абстрактный узор
Абстрактный узор состоит из неузнаваемых форм (линий и форм), необъективного мотива, который нельзя описать никаким другим способом.
Шаблон адаптации
Шаблон адаптации — это шаблон, основанный на другом дизайне, но значительно измененный.
Африканский узор
Также известен как Анкара или Трайбл принт. Африканские узоры имеют яркие, яркие цвета, связанные с африканской культурой.
Рисунок аэрографа
Рисунок аэрографа — это размытый, мягкий, светлый рисунок, который выглядит как созданный с помощью краскопульта художника.
Сплошной узор
Сплошной узор с близкими и равномерно распределенными мотивами.Многие типы узоров используют повторяющиеся узоры.
Рисунок животных
Рисунок животных — это рисунок, похожий на кожу или мех животных. Они могут быть далее разбиты на категории в зависимости от животных, которым пытается подражать рисунок.
Образец гепарда
Образец крокодила
Образец жирафа
Образец ягуара
Образец леопарда
Образец змеи 9
2
Узор-гимн — это классический узор, в котором используются мотивы, похожие на веерообразные пальмовые листья.Узоры Anthemion распространены в греческом и египетском древнем искусстве.
Узор арабески
Узор арабески — это цветочный или геометрический узор, вдохновленный исламским искусством.
Рисунок ар-деко
В орнаментах ар-деко использованы мотивы, типичные для 1920-1930-х годов. В узорах ар-деко используются четкие и четкие линии, геометрические формы и украшения.
Узор в стиле модерн
В узорах в стиле модерн используются динамичные плавные линии, напоминающие цветочные мотивы.Они часто имеют удивительную глубину.
Асимметричный узор
Асимметричный узор — это узор любого типа, в котором отсутствует какая-либо форма симметрии.
Рисунок плетения корзины
Рисунок плетения корзины напоминает плетеную корзину.
Образец батика
Узор батика использует сложные цвета в дизайне, который выглядит так, как будто он был создан путем окрашивания красителем, нанесенным на съемный воск.Узоры батика часто включают в себя природные мотивы (растительность, птицы).
Образец бусинок и катушек
В шаблоне бусин и катушек используются овальные и круглые формы, чередующиеся с удлиненными овалами или цилиндрами.
Рисунок «Птичий глаз»
Рисунок «Птичий глаз» состоит из расположенных маленьких ромбов (обычно четырех) с точкой или промежутком в центре.
Богемный узор
Богемный узор, также называемый принтами бохо или узорами хиппи, отличается яркими цветами и сложными узорами, напоминающими движение хиппи 1960-х годов.
Ботанический узор
Ботанический узор основан на реалистичном изображении растений и трав.
Выкройка Boteh
Выкройка Boteh имеет форму капли с изогнутым верхним концом. Узоры пейсли используют эту форму с дополнительным декором и элементами декора.
Кирпичный узор
Кирпичный узор состоит из последовательных горизонтальных и ломаных вертикальных линий, которые выглядят как кирпичи.
Рисунок «Бычий глаз»
Рисунок «Бычий глаз» состоит из кругов или овалов друг в друге (концентрических).Этот узор часто создает оптические эффекты, такие как движение или пульсация.
Ситцевый узор
Ситцевый узор представляет собой сплошной цветочный узор с использованием ярких цветов. Узор обычно из Индии, но также ассоциируется с тканями в стиле американского кантри.
Камуфляжный узор
В камуфляже используются извилистые узоры, предназначенные для слияния с окружающей средой (камуфляжные узоры в магазине).
Картушный узор
Картушный узор — это продолговатый узор, напоминающий рамку, стол или свиток с надписью.
Узор «Кельтский узел»
Узор «Вечный узел», также называемый узором «Вечный узел», состоит из множества переплетающихся линий или лент, которые плавно соединяются друг с другом и кажутся бесконечными.
Клетчатый узор
Клетчатый узор состоит из горизонтальных и вертикальных полос, которые перекрещиваются друг с другом и образуют узор из квадратов. Существует множество вариантов клетчатого узора.
Шаблон овчарок
Шаблоны овчарок используют небольшие ровные клетки контрастного цвета, обычно черно-белые.
Узор «Аргайл»
Узор «Аргайл» состоит из ромбовидных прямоугольников, расположенных попеременно по диагонали. Узор обычно включает в себя небольшое количество цветов.
Выкройка Бенмора
Выкройка Бенмора — это разновидность районной проверки (Окружная проверка — это образец проверки, похожий на клетчатую клетку. Он состоит из различных схем проверки).
Клетчатый узор буйвола
Клетчатый узор буйвола — это узор в клетку с большими блоками, образованными пересечением двух нитей разного цвета, обычно красного и черного.
Клетчатый узор в клетку
Клетчатый узор в клетку использует квадраты переменного цвета, текстуры или материала.
Округовой узор
Округовой узор — это узор, похожий на тартан. Он состоит из различных шаблонов в клетку. Он возник из мотивов, идентифицирующих шотландские поместья.
Шаблон проверки Dupplins
Шаблон проверки Dupplins — это тип проверки округа (проверки в рамках проверки), в которой используются чередующиеся темные и светлые проверки, часто контуры или обрамленные более светлым узором проверки.
Шаблон проверки Glen
Шаблон проверки Glen — это тип районной проверки, который обычно состоит из сломанных областей проверки на пересечении более темных и светлых полос. Шаблон «Глен чек» также называется чеком принца Уэльского. Обычно используется в костюмах.
Узор «Гинхэм»
Узор «Гинхэм» представляет собой сплошной узор из тканых блоков или клеток, образованных перекрывающимися полосами одинаковой ширины.
Шаблон проверки графика
Шаблон проверки графика состоит из пересекающихся линий на сплошном фоне.Узор напоминает миллиметровую бумагу.
Зуб гончей (узор «гусиные лапки»)
Узор зубцов гончих известен под разными названиями, включая «ломаные», «собачьи», «собачьи», «собачьи» и т. Д. Узор представляет собой сломанные клетки или абстрактные четырехконечные формы, часто черно-белые. Уменьшенная версия рисунка «гусиные лапки» называется щенячьим зубом.
Выкройка в клетку «Мадрас» (клетка)
Выкройка в клетку «Мадрас» — это летний стиль ткани, отличающийся рисунком в красочную клетку и полосы.Полосы медресе в клетку или плед состоят из полос разного цвета, которые пересекаются друг с другом, образуя неровные клетки.
Образец мини-проверки
Образец мини-проверки состоит из очень мелких проверок. Размер чеков находится между чеками в мелкую клетку и чеками в клетку.
Шаблон проверки булавки
В шаблоне проверки булавки используются пересекающиеся полосы размером с булавку толщиной всего в одну или две нити.
Плед
Термины тартан, плед и клетка часто используются как синонимы.Сегодня тартан относится к разновидности клетчатого узора. Пледы состоят из скрещенных горизонтальных и вертикальных полос двух и более цветов. Основное отличие традиционных тартанов от других видов пледов заключается в повторении узора. Что касается пледов, узор вертикальной полосы не обязательно должен совпадать с рисунком горизонтальной полосы, как узор тартана.
Шаблон проверки «пастырь»
Также известный как проверка «мешок с губкой», образец проверки «пастырь» представляет собой тип районной проверки, который включает небольшие, даже двухцветные проверки.
Узор «Таттерсейл»
Узор «Таттерсейл» — это узор в клетку или клетку, в котором равномерно расположенные, тонкие, даже вертикальные полосы, повторяющиеся по горизонтали, образуют квадраты. Полосы обычно имеют чередующиеся цвета и обычно расположены на светлом фоне.
Шаблон проверки оконного стекла
Шаблон проверки оконного стекла напоминает панели в окне. Узор представляет собой широкие квадратные клетчатые узоры в виде окон.
Выкройка Chinoserie
Выкройка Chinoserie включает принты китайского шрифта, обычно изображающие китайскую архитектуру, лодки и другие объекты, явно китайские.
Рождественский узор
Рождественский узор описывает множество узоров, основанных на рождественской теме, таких как звезды, олени, падуб и т. Д., Обычно с использованием зеленого и красного цветов.
Узор из точек в виде монет
Узор из точек в виде монет — это узор из точек в горошек, в котором используются очень большие точки (например, монеты).
Образец коллажа
Узор коллажа напоминает обрывки, фотографии, рисунки или другие объекты, наклеенные на ткань.
Составной шаблон наложения
В составном шаблоне наложения используются два или более шаблонов, наложенных друг на друга.
Составной шаблон повторения
В составном шаблоне повторения используются два или более шаблонов различных типов, которые повторяются.
Контурный узор
Контурный узор — это узор, который выделяет блики фигур или фигур.
Шаблон разговора
Шаблоны разговора — это отпечатки объектов, на которых изображены узнаваемые объекты (например, животные) в мотиве.
Коралловый узор
Коралловый узор — это узор, напоминающий кораллы.
Шаблон встречного обмена
Шаблон встречного обмена — это узор с перевернутыми узором и фоном в другой части рисунка.
Дамасский узор
Дамасский узор — классический принт с цветочными мотивами. Обычно он одноцветный и часто печатается на шелке или шерсти.
Дизайнерский узор
Дизайнерский узор — это единственный в своем роде узор, который обычно защищен авторским правом.
Диагональный узор
На диагональном узоре ткани присутствуют диагональные линии.
Ромбовидный узор
Ромбовидный узор состоит из ромбов.
Рисунок подгузника
Рисунок подгузника состоит из небольших переплетенных, близко расположенных форм, обычно некоторого типа ромбовидного рисунка.
Цифровой узор
Цифровой узор — это узор, созданный с помощью элементов, сгенерированных компьютером.Они часто художественно пикселизированы или имеют фрактальные формы.
Рисунок направленности
Шаблон направления — это любой рисунок, в котором мотивы ориентированы в одном или нескольких конкретных направлениях.
Ditsy pattern
Также называемый Ditsies, ditzy или ditsie, ditsy-узор представляет собой сплошной узор из мелких пятен, кругов, зигзагов или других элементов, который выглядит случайным.
Рисунок зубов собаки
Рисунок зубов собаки, также называемый собачьим зубом (гусиные лапки), представляет собой небольшие зубчатые ячейки, обычно образованные четырехконечными звездами.
Пунктирный швейцарский узор
Пунктирный швейцарский узор представляет собой узор, сделанный из небольших выпуклых точек. Узор обычно используется на тонкой ткани, которая контрастирует с более толстыми узорами в виде точек.
Рисунок сухой кистью
Рисунок сухой кисти выглядит так, как будто он был создан кистью художника, на которой было только небольшое количество краски, что создает царапающий текстурированный вид.
Эксцентричный узор
Эксцентричный узор — это узор, состоящий из тонких линий, создающих эффект поп-арта.
Рисунок «Яйцо и дротик»
Рисунок «Яйцо и дротик» — это классический рисунок, в котором овальный элемент чередуется с элементом в виде заостренной стрелки.
Разработанный узор
Разработанный узор — это узор или группа мотивов, специально разработанных для соответствия форме.
Этнический образец
Этнический образец является репрезентативным или общим для какой-либо культуры. Их можно разбить на следующие типы этнических паттернов.
Ацтекский узор
Килм узор
Навахо узор
Сузаани
Племенной узор
Узор с вечными узлами, узоры с вечными узлами
2
как узел переплетенных лент, плавно переходящих друг в друга.
Образный узор
Образный узор состоит из элементов человека или животных, часто исторических фигур.
Узор «Флер де Лис»
Узор «Флер де Лис» представляет собой стилизованный узор из трех или четырех лепестков лилии. Изначально это был символ чистоты.
Цветочный узор
Цветочный узор включает цветочные мотивы, такие как цветы, стручки семян, листья (цветочные узоры из магазина).
Рисунок ладов
Рисунок ладов состоит из взаимосвязанных и симметричных геометрических мотивов. Его также называют паттерном «Греческий ключ».
Образец платка
Узор платка — это базовый образец повторения блока в мелком масштабе.Типичные варианты состоят из повторяющихся геометрических фигур.
Шаблон четырехстороннего макета
В четырехстороннем шаблоне есть мотивы, обращенные во всех четырех направлениях (влево, вправо, вверх, вниз).
Фризный узор
Фризный узор — это узор, который повторяется в одном направлении, например, переплетенная веревка или удлиненная лоза.
Геометрический узор
Геометрический узор — это повторяющийся узор геометрических фигур (например, ромбов, квадратов, кубов).
Шаблон градации
Шаблон градации — это узор с различными размерами, цветами или формами.
Графический узор
Графический узор — это отпечатки, основанные на графическом искусстве.
Греческий ключевой узор
Греческий ключевой узор включает взаимосвязанные и симметричные геометрические мотивы. Его еще называют ладовым узором.
Гильошированный узор
Гильошированный узор — это узор из чередующихся изогнутых полос.Иногда узор предназначен для образования кругов.
Образец полос по линии роста волос
Образец полос по линии роста волос состоит из очень тонких полос, примерно шириной с человеческий волос.
Половина капли
Полукапля похожа на кирпичную, но в основном с вертикальными линиями. Мотив повторяется примерно на полпути сбоку.
Арлекинский узор
Арлекинский узор — это повторяющийся узор из контрастирующих ромбов или продолговатых квадратов в виде решетки.
Гавайский узор
Гавайский узор в любом узоре, который включает гавайские культурные мотивы (например, ананасы, океан). Они часто бывают с цветочными узорами и ярко окрашены.
Узор Герати
Узор Герати представляет собой розетку, заключенную в ромб с зубчатым листом по бокам. Его название происходит от города Герат в Афганистане, откуда он первоначально произошел.
Шестиугольный узор
Шестиугольный узор использует шестиугольные формы во всей сети.
Рисунок «Елочка»
Рисунок «Елочка», также называемый шевронным узором, представляет собой мотив из зигзагообразных полос.
Рисунок зубов собаки
Рисунок зубов собаки (гусиные лапки) состоит из небольших ломаных зубчатых клеток, образованных четырехконечными звездами.
Выкройка икат
Выкройка икат использует нити, которые окрашиваются перед ткачеством для создания выкройки.
Иллюзионный узор
Иллюзионный узор — это любой тип узора, создающий оптическую иллюзию.Они часто создаются с помощью очень маленьких близко расположенных линий.
Шаблон взаимосвязи
В шаблоне взаимосвязи мотивы тесно связаны друг с другом. С этим узором движение одного мотива не может происходить без воздействия на другой.
Нерегулярный шаблон повторения
Нерегулярный шаблон повторения аналогичен шаблонам с половинной каплей и кирпичной кладкой, за исключением того, что последовательные элементы немного перемещаются на заданное расстояние.
Якобский узор
Якобский узор — это узор вышивки с цветами, птицами.
Пейзаж
Пейзажный рисунок включает пейзажные сцены.
Сетчатый узор переулка
Сетчатый узор переулка представляет собой узор из ромбовидных мотивов, каждый ромб повернут на 45 и 90 градусов и обычно заполнен тонкими линиями, расходящимися с противоположных концов.
Решетчатый узор
Решетчатый узор — это взаимосвязанный крестообразный узор с квадратами или ромбовидными отверстиями.
Образец стиля Либерти
Образец стиля Либерти представляет собой сплошной узор с мелкими цветочными узорами, которые очень стилизованы.Узор был создан (и назван в честь) компанией Liberty & Co (Лондон).
Шаблон логотипа
Шаблон логотипа — это любой рисунок, созданный из логотипа.
Мадрасский узор
Мадрасский узор — это клетчатый узор с яркими цветными полосами, клетками или клетками, которые переходят друг в друга.
Металлический узор
Металлический узор — это узор, похожий на простроченное квилт: либо простеганный, либо набивной.
Шаблон в мини-клетку
Шаблон в мини-клетку — это шаблон, сделанный из очень маленьких клеток. Размер чеков находится между чеками в мелкую клетку и чеками в клетку.
Муаровый узор
Муаровый узор состоит из волн и ряби, созданных наложением двух или более простых мотивов.
Мозаичный узор
Мозаичный узор состоит из множества маленьких цветных кусочков. Кусочки обычно имеют примерно квадратную форму, но могут быть искажены или деформированы в виде квадратов, прямоугольников или полностью других форм.
Естественный или натуралистический узор
Натуральный или натуралистический узор с естественными мотивами, такими как волны, деревья, горы.
Аккуратный узор
Аккуратный узор — это сплошной узор с мелкими, цветочными или геометрическими мотивами в одном или двух цветах.
Сетевой шаблон
Сетевой шаблон представляет собой повторяющуюся комбинацию прямоугольников, квадратов и значков.
Выкройка детской комнаты
Выкройка детской комнаты — это любой рисунок, содержащий детские элементы, такие как игрушки, плюшевые мишки или предметы ухода за младенцами.
Образец Ogee
Ogee — это кривая, имеющая форму буквы «S», с дугами, изгибающимися в противоположных смыслах. Узор ogee содержит узоры ogee, образующие несколько луковичный мотив.
Рисунок «Омбре»
Рисунок «Омбре» — это эффект оттенка с постепенным переходом от темного к светлому и от открытого к закрытому по покрытию.
Восточный узор
Восточный узор — это замысловатый узор, обычно медальон, из индийской культуры.
Общий рисунок
Общий рисунок — это тип макета рисунка с близкими и равномерно распределенными мотивами, обычно покрывающими всю ткань с небольшим видимым фоном.
Узор «Пейсли»
Узор «Пейсли» используют стилизованные узоры в форме слезы с изогнутыми верхними концами. Узоры Пейсли могут быть любого масштаба, разноцветными, монохромными, простыми или сложными, в регулярном и повторяющемся или разнообразном, нерегулярном и, казалось бы, случайном узоре.Узор был первоначально создан в (и получил свое название от) Пейсли, Шотландия.
Узор из пальметты
Узор из пальметты представляет собой стилизованную версию веерообразных листьев пальмы.
Патриотический узор
Патриотический узор — это тема, представляющая определенную страну.
Узорчатый узор фона
Узорчатый узор фона описывает цвет фона, который сам по себе является узором (часто полосы, точки, зигзагообразные линии, пледы или геометрические фигуры).
Образец полосок карандаша
Образцы полосок карандаша — это узор из полосок, состоящий из линий примерно такой же ширины, как нарисованные карандашом.
Шаблон для домашних животных
Шаблоны для домашних животных содержат мотивы домашних животных (например, собак, кошек, хомяков).
Рисунок «Глаз фазана»
Рисунок «Глаз фазана» — это тип переплетения, образующий ромбовидную форму, немного больше, чем рисунок «птичий глаз».
Узор «Pincheck»
Узор «Pincheck» представляет собой пересекающиеся полосы размером с булавку толщиной всего в одну или две нити.
Точечный узор
Точечный узор — это узор из очень маленьких точек в горошек.
Узор в тонкую полоску (или полоску)
Узор в тонкую полоску представляет собой узор из полосок с непересекающимися, но иногда прерывистыми тонкими линиями толщиной всего в одну или две нити.
Плед
Плед состоит из пересекающихся цветных полос, обычно пересекающихся под прямым углом. Пледы состоят из скрещенных горизонтальных и вертикальных полос двух и более цветов.Основное отличие традиционных тартанов от других видов пледов заключается в повторении узора. Что касается пледов, узор вертикальной полосы не обязательно должен совпадать с рисунком горизонтальной полосы, как узор тартана.
Шаблон в горошек
В шаблоне в горошек используются повторяющиеся точки, расположенные на одинаковом расстоянии друг от друга, обычно одинакового размера.
Паттерн в стиле поп-арт
Паттерн в стиле поп-арт — это паттерны графических изображений повседневных предметов, характерные для того времени.
Позитивно-отрицательный узор
При положительно-отрицательном паттерне как мотив (положительное пространство), так и окружающая область (отрицательное пространство) имеют идентичные формы.
Четырехлистник
Четырехлистник, который выглядит как четыре частично перекрывающихся круга одинакового размера. Узор чем-то похож на серию мотивов четырехлистного клевера (слово «четырехлистник» означает «четыре листа»).
Случайный узор
Случайный узор, также называемый рисунком с перебрасыванием, включает элементы, которые кажутся случайными разбросанными по ткани.
Полосы в стиле Регентства
Полосы в стиле Регентства, также называемые бенгальскими или тигровыми полосками, представляют собой полосы одинаковой ширины, чередующиеся светлые и темные цвета. Полоски шире, чем у конфет, но тоньше, чем у тентов.
Полковая нашивка
Полковая нашивка состоит из полос, окрашенных в цвета британских полков. Полосы обычно состоят из комбинации толстых, тонких и тонких линий.
Ретро-узор
Ретро-узор — это любой узор из предыдущего модного тренда.
Рисунок в римские полосы
Рисунок в римские полосы — это яркие разноцветные вертикальные полосы, которые сильно контрастируют друг с другом.
Сатиновый узор повторения
Также известный как точечный повтор, шаблон сатинового повторения включает мотивы, расположенные на сетке, так что каждое пространство сетки содержит только один экземпляр мотива (хотя мотивы могут быть повернуты в разных направлениях).
Масштабный узор
Масштабный узор, также называемый раскладушкой, состоит из перекрывающихся дуг, которые выглядят как чешуя рыбы или змеи (в форме моллюска).
Узор прокрутки
Узор прокрутки содержит спиральные формы и кривые, похожие на виноградные лозы.
Бесшовные шаблоны
Бесшовные шаблоны — это любой рисунок, в котором все мотивы соприкасаются друг с другом.
Узор из серпантинных полос
Узор из серпантинных полос содержит выровненные, волнистые, синусоидальные полосы.
Клетка овчарки
Также известная как клетка губчатого мешка, клетка пастыря представляет собой разновидность окружной проверки, которая включает небольшие ровные клетки двух цветов.
Образец эскиза
Узор эскиза, также известный как узор «крокис», представляет собой раскрашенный узор, который не повторяется. сетка, так что каждое пространство сетки содержит только один экземпляр мотива (хотя мотивы могут быть повернуты в разных направлениях).
Образец веточек
Рисунок веточек выглядит как повторяющиеся веточки и маленькие побеги молодых веток.
Квадратный узор повторения
Квадратный повтор, также называемый блочным повтором, прямолинейным повтором, прямым повтором и полным повторением, представляет собой повторяющийся мотив, который появляется слева и справа от исходного элемента.
Точечный узор
Точечный узор использует точки, расположенные очень близко друг к другу, чтобы создать уникальный текстурированный элемент или закрашенный узор.
Прямой поперечный или прямой узор повторения
Прямой поперечный или прямой повторный узор, также называемый блочным повтором, квадратным повтором и полным повторением, представляет собой повторяющийся мотив, который появляется слева и справа от исходного элемента.
Рисунок из штрихов
Рисунок из бороздок состоит из полос, которые переходят по цвету или текстуре в одном направлении.
Образец полос
Узор маркизы
Узор маркизы представляет собой широкие вертикальные однотонные полосы на светлом фоне.
Шаблон штрих-кода
В шаблоне штрих-кода используются повторяющиеся черные полосы различной ширины на белом фоне, который выглядит как штрих-код продукта.
Баядерский узор
В баядерском узоре используются яркие горизонтальные полосы разной ширины
Бенгальский узор
Бенгальский узор, также называемый полосами Регентства, состоит из полос одинаковой ширины, чередующихся темных и светлых цветов. Полосы шире, чем полосы конфет, но уже, чем полосы тента.
Бретонский узор с полосками
Характерный бретонский узор с горизонтальными черными или сине-белыми полосами.
Конфеты с рисунком
Конфеты с рисунком в виде полосок равного размера, как правило, вертикальные, с использованием яркой цветной полосы с белой полосой.
Шевронный узор
Шевронный узор, также называемый «елочкой», представляет собой узор из зигзагообразных полос.
Выкройка платья
Выкройка платья состоит из полос разного цвета и ширины.Ширина полосы обычно включает толстую полосу, ограниченную более тонкой полосой с каждой стороны.
Волосный узор
Волосный узор состоит из серии очень узких полос.
Горизонтальные или вертикальные линии
Многоцветный узор
Узор в полоску (или полоску)
Узор в полоску — это узор из полосок с непересекающимися, но иногда прерывистыми тонкими линиями толщиной всего в одну или две нити .
Полковая модель
Полковая нашивка состоит из полос, окрашенных в цвета британских полков.Полосы обычно состоят из комбинации толстых, тонких и тонких линий.
Римский узор
Римский узор — это яркие разноцветные вертикальные полосы, которые сильно контрастируют друг с другом.
Змеевик
Змеевик состоит из выровненных волнистых синусоидальных полос.
Шаблон теневых полос
Шаблон теневых полос представляет собой полосы, которые обычно различаются по ширине и обычно состоят из двух или более цветов.
Вихревой узор
В вихревом шаблоне используются круговые вихревые мотивы.
Рисунок тартана
Термины «тартан», «плед» и «клетчатый рисунок» часто используются как синонимы. Сегодня тартан относится к разновидности клетчатого узора. Основное отличие традиционных тартанов от других видов пледов заключается в повторении узора. Что касается тартанов, рисунок вертикальной полосы обычно совпадает с рисунком горизонтальной полосы.
Узор «Таттерсейл»
Узор «Таттерсейл» представляет собой мелкие клетчатые узоры с равномерно расположенными, равномерно окрашенными тонкими линиями.
Шаблон мозаики
Шаблон мозаики — это повторяющийся шаблон взаимосвязанных форм, которые можно бесконечно расширять.
Узор текстуры
Узор текстуры — это узор, который выглядит как поверхность известного объекта, например дерева, гранита, камня или других материалов.
Узор «Тойль-де-Жуой»
Узор «Тойль-де-Жуой» выполнен в цветочной тематике, характерной для сельской местности Франции, и обычно одного цвета на светлом или белом фоне.
Шаблон с метками
Шаблон с метками, также называемый случайным образом, использует элементы, которые случайным образом разбросаны внутри блока.
Ажурный узор
Ажурный узор похож на переплетение каменных, деревянных или железных столбов, удерживающих стекло в готическом окне.
Рисунок «Трилистник»
Рисунок «Трилистник» представляет собой рисунок из трех лепестков или трех лепестков. В отличие от четырехлистника с четырьмя «листиками».
Шаблон «Решетка»
В шаблоне «Решетка» используются взаимосвязанные элементы, похожие на деревянную или металлическую решетку (для поддержки виноградных лоз). Иногда в мотив включаются виноградные лозы.
Двухцветный узор симметрии
Двухцветный узор симметрии, также называемый рисунком встречной замены, представляет собой узор с перевернутыми узором и фоном в другой части узора.
Двунаправленный узор или Двухсторонний узор раскладки
При двунаправленном узоре (или двухстороннем узоре раскладки) половина мотивов обращена в противоположном направлении.
Рисунок несбалансированных полос
Рисунок несбалансированных полос состоит из повторяющихся асимметричных, но несбалансированных полос.
Ненаправленный шаблон
Ненаправленный шаблон — это шаблон, который выглядит одинаково с любого направления.
Вермикулярная структура
Вермикулярная структура содержит неправильные скрученные линии, напоминающие изогнутых червей.
Винтажный узор
Винтажный узор — это любой исторический узор.
Акварельный узор
Акварельный узор выглядит как акварель (акварель). Часто используют светлые, мягкие градации.
Шаблон проверки оконного стекла
Шаблон проверки оконного стекла содержит широко расставленные флажки, напоминающие оконные стекла. Рисунок распространен на костюмах и рубашках.
Венок
Венок содержит круговые узоры из переплетенных цветов или листьев.В их состав часто входят ленты и другие украшения.
Зигзагообразный узор
Зигзагообразный узор представляет собой неровные, соединенные под углом прямые линии, которые образуют чередующиеся резкие повороты.
Как это:
Нравится Загрузка …
Блоки шаблонов +
Описание
Примеры
Файлы примеров
Особенности инструмента
Сочетания клавиш
Ссылки
Описание
Инструмент Pattern Blocks + Tool — это виртуальный инструмент, похожий на физические, обычно доступные в классах.Восемнадцать различных фигур можно перетащить в рабочую область с прокручиваемой панели выбора слева. Попав в рабочую область, их можно перемещать, копировать, отражать или вращать по отдельности или группами. Включены блоки для представления десятых долей. Цвет каждого типа блока можно изменить. Студенты могут разрабатывать и разрабатывать многочисленные математические концепции. В рабочем пространстве Pattern Blocks + отображается изометрическая сетка из маленьких равносторонних треугольников, которая уникальна, когда квадратная сетка используется для многих видов деятельности (см. Обсуждение единиц длины и площади в разделе «Измерение и геометрия» ниже).
Доступ к широкому спектру инструментов аннотации для передачи мышления.
Вставьте изображения в инструмент.
Работа, созданная в математическом инструменте, может быть сохранена и открыта.
Сохраненным файлом можно поделиться с коллегами или передать учителю. Файл будет содержать все шаги решения от начала до конца.
Сделайте снимок экрана, чтобы использовать его как часть портфолио, презентации, веб-страницы и т. Д.
вверху
Математические концепции
Блоки паттернов могут быть использованы для развития понимания:
- геометрических отношений (включая составление и разложение фигур)
- паттерны (включая повторяющиеся паттерны, паттерны линейного роста и паттерны с 1 или 2 атрибутами)
- Измерение длины и площади (включая периметр и использование нестандартных единиц)
- свойства многоугольников и углов (включая симметрию)
- преобразования (переводы, отражения, вращения и расширения)
- соответствие и сходство
- дроби и десятичные дроби (включая представление, сравнение, порядок, эквивалентность и операции)
- мозаика
- переменные, выражения и уравнения
наверх
Соединение фундаментальных математических понятий с блоками шаблонов +
| Фундаментальные концепции и навыки (Ссылка № 1) | Узорчатые блоки + соединения |
|---|---|
| Работа с номерами: Понимание и использование чисел (например,g., способность читать, представлять, считать, упорядочивать, оценивать, сравнивать, составлять, разлагать и перекомпоновывать числа). | Pattern Blocks + можно использовать для:
|
| Распознавание и применение понимания свойств числа: Понимание того, как числа ведут себя в операциях, и использование этого понимания для усвоения математических фактов и выполнения вычислений. | Pattern Blocks + можно использовать для:
|
| Освоение математических фактов: Понимание и запоминание математических фактов с использованием различных стратегий. | Pattern Blocks + можно использовать для:
|
| Развитие умственных математических навыков: Выполнение расчетов в уме, практически без использования бумаги, карандаша или калькулятора. | Использование визуальных инструментов при обучении выполнению математических операций позволяет учащимся использовать эти ментальные модели и визуализации для выполнения мысленных вычислений. Студенты будут развивать свои умственные математические навыки с
|
| Повышение квалификации с помощью операций: Выполнение вычислений с легкостью, точностью и согласованностью, а также с общим пониманием чисел и операций, свойств чисел и их соответствующего применения при решении проблем. | Pattern Blocks + можно использовать для:
|
Соединение фундаментальных математических понятий с математикой.ca (Осадка)
наверх
Примеры
Дизайн
Учащиеся развивают чувство пространства, создавая конструкции и копируя или изменяя существующие конструкции.
Возможные виды деятельности:
- Создайте изображение цветка с помощью блоков узора.
Примечание: Это пример задачи из математического ожидания 1-го класса «Геометрия и пространственное восприятие — геометрические отношения»: составлять узоры, изображения и рисунки, используя общие двумерные формы - Составьте шестиугольник, используя разное количество меньших фигур.
Примечание: Это пример задачи из математического ожидания 3-го класса «Геометрия и пространственное восприятие — геометрические отношения»: решать задачи, требующие наибольшего или наименьшего количества двумерных форм (например, блоков узора), необходимых для создания более крупной формы в различными способами (например, чтобы прикрыть контурную головоломку) - Создайте дизайн ниже:
- С помощью приведенного ниже шаблона динозавра учащиеся могут:
- откройте образец файла с серым изображением и закройте его блоками.Студентов можно попросить использовать наибольшее и наименьшее количество блоков или наибольшее количество различных блоков.
На рабочем столе щелкните изображение выше, чтобы открыть этот файл.
- откройте образец файла с серым изображением и закройте его блоками.Студентов можно попросить использовать наибольшее и наименьшее количество блоков или наибольшее количество различных блоков.
- С помощью серой лодки, изображенной ниже, учащиеся могут:
- Постройте форму, сказав, что она похожа на коричневый блок лодки, но с боковыми сторонами, которые в два раза длиннее.
(старшие ученики могли сделать выводы об углах в этих двух похожих формах) - откройте образец файла с серым изображением и закройте его блоками.
Студенты могут применять разные правила (например, закрывающие блоки могут выходить за пределы изображения, закрывающие блоки могут перекрываться, зазоры не допускаются).На рабочем столе щелкните изображение выше, чтобы открыть этот файл. - открыть файл, в который их учитель добавил вопросы.
- поместите коричневый блок в разные места и найдите центр расширения, в котором будет получено серое изображение.
- создайте свою собственную головоломку с серым контуром и предложите одноклассникам решить ее различными способами (см. инструкции).
- Постройте форму, сказав, что она похожа на коричневый блок лодки, но с боковыми сторонами, которые в два раза длиннее.
- Поищите в Интернете шаблоны плитки, которые можно создать с помощью Pattern Blocks +.Статья в Википедии о мозаиках многоугольников — хорошее место для начала. Опишите ядро паттерна и преобразования, необходимые для расширения паттерна. Определите полученные симметрии (см. Три дополнительных примера в разделе «Геометрические свойства» ниже).
верх
Number Sense
Многие действия по подсчету WINS можно использовать с блоками шаблонов + (щелкните ссылку «Действия», чтобы развернуть список).
Подсчитайте количество различных типов блоков в дизайне.
Составление и разложение чисел
См. Действия WINS для составления и разложения чисел до 5, чисел до 10 и чисел до 20.
Номера для сравнения и заказа
См. Действия WINS для сравнения и упорядочивания чисел до 10 и чисел до 20.
верх
Геометрические свойства
Сортировка коллекции фигур по их геометрическим свойствам.
(например, количество сторон, длина сторон, количество внутренних углов, количество прямых углов, площадь, периметр, симметрия)
Студентов можно спросить, как была организована вышеуказанная сортировка.
Приведенная выше сортировка с использованием диаграммы Венна поднимает несколько интересных вопросов:
- Может ли четырехугольник не иметь параллельных сторон? Если да, используйте функцию аннотации, чтобы нарисовать ее.
- Какие еще общие классификации форм не представлены блоком узора? (е.г., равнобедренные треугольники)
Создайте новые блоки узоров, чтобы представить некоторые из этих форм. (например, равнобедренный треугольник с двумя углами 45 °)
Вызовы:
- Можно ли создать четырехугольник без параллельных сторон, состоящий из блоков узора?
Может помочь рассуждение об использовании внутренних углов блоков выкройки.
Зависит ли ответ от того, разрешено ли перекрытие блоков? привязать к сетке? - Создайте новый блок шаблона, который представляет собой четырехугольник без параллельных сторон.
Используйте бумагу с треугольной изометрической сеткой (см. Dynamic Paper NCTM), программное обеспечение для динамической геометрии или программное обеспечение для 2D-дизайна, если оно доступно.
Возможное решение : Блокнот для рисования Геометра был использован для создания четырехугольного блока сливового цвета.
Приведенный ниже дизайн был затем создан:
- Вставкой изображения четырехугольного блока сливового цвета в инструмент Узорчатые блоки +.
- Перетаскивание красного блока трапеции в рабочую область; поворот и изменение размера изображения сливового блока в соответствии с длиной одной стороны красной трапеции.
- Копирование изображения блока сливы и размещение его рядом с исходным изображением.
- Перетаскивание и размещение других блоков.
Примечание : два оранжевых квадратных блока и зеленый треугольный блок помещены поверх изображения сливового блока. Отключите привязку к сетке, чтобы разместить эти блоки по углам сливового блока. Эти угловые блоки помогают нам видеть углы 90 °, 60 °, 90 ° в трех углах блока сливового цвета. Какова мера четвертого угла?
Создайте и определите конгруэнтные формы.
В Pattern Blocks + конгруэнтные формы создаются путем копирования, преобразования, отражения и поворота фигур.
Студентов также можно попросить:
- создавайте каждый дизайн, используя Pattern Blocks +
- описать некоторые из преобразований, замеченных в дизайне
- найти форму ядра, которую можно многократно трансформировать для создания каждого шаблона дизайна
Примечание: Первая фигура выше доступна как образец файла.Отменить и повторить последовательность действий, чтобы увидеть, как можно идентифицировать ядро и применить преобразования.
Угадай мою форму.
Студенты работают в партнерах. Каждый ученик создает форму, используя блоки узора, скрытые от взгляда своего партнера. Затем ученики по очереди дают подсказки, которые описывают их форму, используя правильную математическую терминологию. Основываясь на подсказке, партнер пытается повторить форму. Студенты продолжают обмениваться подсказками, пока каждый партнер не сможет воспроизвести форму другого.
Некоторые примеры подсказок для вышеуказанной формы:
- Форма состоит из шести блоков.
- Каждый блок имеет одну сторону ровно с двумя другими блоками.
- Все шесть блоков совпадают.
- Имеется более 4 линий симметрии.
Каков периметр этой формы? (Этот вопрос может вызвать оживленную математическую дискуссию!)
наверху
Узор
Выявление, расширение и создание повторяющихся шаблонов.
Учащиеся демонстрируют понимание того, что закономерности возникают в результате использования трансформации (например, скольжение, переворачивание, поворот) или повторного изменения атрибута (например, формы, размера и т. Д.).
цвет, ориентация, номер).
Примечание: В шаблонных блоках все блоки с заданной формой имеют одинаковый цвет, что ограничивает количество атрибутов, которые могут изменяться. Чтобы создать узоры с большим количеством атрибутов, рассмотрите возможность использования инструмента «Установить».
Учащиеся расширяют и создают повторяющиеся узоры в результате отражений и / или вращений.
Создайте составной поезд шаблона, чередуя один зеленый треугольник с одной красной трапецией. Угадайте, какой блок окажется на 30-м месте.
Примечание: Это пример задачи из математического ожидания 4-го класса «Паттерны и алгебра — паттерны и взаимосвязи»: делать прогнозы, связанные с повторяющимися геометрическими и числовыми паттернами
Выявление, расширение и создание моделей роста.
На изображении показаны первые 3 члена линейной модели роста.
Как будет выглядеть 10 семестр?
Сколько блоков будет в 10-м триместре?
Сколько блоков будет в сотом семестре?
Существует ли термин, содержащий 45 блоков? 300 блоков?
Учащиеся создают визуальные представления линейных моделей роста, затем задают вопросы и отвечают на вопросы по каждой модели.
верх
Измерения и геометрия
Учебный план Онтарио (ссылка № 2) предлагает использовать блоки физических шаблонов в качестве нестандартных единиц длины, площади и объема.
Покрывающий дизайн (см. Выше) также отвечает разнообразным требованиям к геометрии, содержащимся в учебной программе Онтарио.
Учащиеся измеряют составные формы и соотносят их с длинами сторон, площадями и углами основных блоков.
Единицы длины и площади, используемые с блоками массива
Инструмент Pattern Blocks + использует треугольную изометрическую сетку.
Типичная единица длины — это расстояние между соседними точками, которое представляет собой длину стороны первых шести стандартных блоков шаблона.
Типичная площадь единиц — это площадь маленького зеленого треугольника.
При использовании квадратной сетки размером 1 см на 1 см длины обычно измеряются в сантиметрах, а площади — в квадратных сантиметрах.
На сетке Узорчатые блоки + ниже площадь маленького зеленого треугольника не равна квадрату длины его стороны. Это оранжевый блок, площадь которого равна квадрату длины его стороны.
Площадь квадрата более чем в два раза превышает площадь треугольника. Подсказка: Проведите вертикальную линию через середину фигуры.
Точнее, площадь маленького зеленого треугольника составляет около 43% площади оранжевого квадрата.
Площадь желтого шестиугольника — два подхода
Когда мы говорим, что площадь желтого шестиугольника равна 6, мы имеем в виду 6 маленьких зеленых треугольников.
Однако площадь желтого шестиугольника, измеренная в оранжевых квадратах, меньше 4, как показано на изображении ниже.
Площадь желтого шестиугольника на самом деле меньше трех оранжевых квадратов.
Подсказка: Сравните площадь шестиугольника, который не находится над квадратами, с площадью квадратов, который не находится под шестиугольником.
При измерении очень важно четко понимать, какие единицы измерения используются. Желтый шестиугольник имеет размер 6, когда площадь маленького зеленого треугольника равна единице. Однако его размер составляет примерно 2,6, когда используется квадратная сетка.
верх
Пример 1 — Наибольший периметр для фиксированной площади
Создайте составную форму из шести желтых шестиугольников с максимально возможным периметром.
Поощряйте учащихся использовать эффективные вычислительные стратегии для расчета периметров.
Расширения:
- Измените количество блоков, разрешенных для создания составной формы.
- Изменить тип блоков, разрешенных для создания составной формы.
- Создавайте составные формы с максимально возможной площадью по заданному периметру.
- Определите углы 60 °, 120 °, 240 ° и 360 ° в созданных составных формах.
вверху
Пример 2 — Связь площади треугольника, параллелограмма и прямоугольника
Отнесите площадь треугольника к параллелограмму.
Причина, по которой параллелограмм (в данном случае ромб) в два раза превышает площадь большого зеленого треугольного блока:
- Признавая, что параллелограмм состоит из двух одинаковых больших зеленых треугольных блоков
- подсчитывая количество маленьких зеленых блоков в каждом (9 и 18)
Отнесите площадь треугольника к прямоугольнику.
- Используйте функцию аннотации, чтобы нарисовать синий прямоугольник вокруг светло-зеленого треугольника. Нарисуйте сплошные треугольники в белом пространстве. Поверните их, чтобы они поместились внутри треугольника.
- Причина в том, что прямоугольник в два раза больше светло-зеленого треугольника.
Отнесите площадь параллелограмма к прямоугольнику.
- Причина в том, что площадь параллелограмма равна площади прямоугольника, поскольку оба они вдвое больше светло-зеленого треугольника.
- Используйте маленькие зеленые блоки, чтобы убедиться, что количество блоков, необходимое для покрытия параллелограмма, также покроет прямоугольник.
Подобно многим упражнениям, связанным с блоками шаблонов, это упражнение предназначено для того, чтобы дать учащимся вводный, интуитивный опыт взаимоотношений областей, указанных выше, который затем может быть распространен на более общие случаи.
верх
Пример 3 — Угловые меры
Определите внутренние и внешние углы всех блоков рисунка, соотнося их с внутренними углами равностороннего треугольника, равными 60 °.
Например, выведите, что углы желто-коричневого ромба равны 30 ° и 150 °.
Проверить свойства, в том числе:
- прямой угол 180 °
- сумма углов в треугольнике равна 180 °
- сумма углов в четырехугольнике до 360 °
- внешний угол треугольника равен сумме двух противоположных внутренних углов
вверху
Пример 4 — Похожие рисунки
Соотнесите площади и периметры одинаковых форм.
Например:
- серая лодка в два раза превышает периметр коричневого блока лодки и в четыре раза больше его площади.
- периметр большого светло-зеленого блока в три раза больше периметра маленького темно-зеленого блока и в девять раз больше его площади.
верх
Пример 5 — Высота равностороннего треугольника
Примечание: Когда одна сторона треугольника определяется как основание ,
тогда отрезок, перпендикулярный основанию, содержащий противоположную вершину, называется высотой или высотой треугольника.
В 7 классе ученики узнают, что независимо от того, какая сторона считается основанием, площадь равна половине длины основания, умноженной на высоту от этого основания.
Отнесите высоту зеленого треугольного блока к длине его стороны.
Щелкните изображение выше, чтобы увидеть его в полном размере, без искажений.
На основании каждого пронумерованного термина выше причина того, что высота равна:
- меньше длины его стороны
- более половины длины его стороны
- более двух третей длины его стороны
- более трех четвертей длины его стороны
- более четырех пятых длины его стороны
- более пяти шестых длины его стороны
- действительно близко к шести седьмым его длина стороны
- менее семи восьмых длины его стороны
Используйте теорему Пифагора, чтобы связать высоту зеленого треугольного блока с длиной его стороны.
Разница между оценкой в шесть седьмых и фактическим значением составляет менее 1%.
Создайте различные числовые шаблоны из указанной выше последовательности.
- количество квадратов
- количество треугольников
- количество блоков шаблона
Решите связанные проблемы (например, какой следующий член, 20-й член, общий член).
Интересные факты о треугольниках
(которые имеют очень мало общего с блоками шаблонов)
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника.Эта точка является центром круга, который можно построить, создав треугольник со сторонами, параллельными исходному треугольнику, через его вершины (см. Ниже).
Другие «центры» треугольника включают в себя центр окружности, центр и центроид, хотя для равностороннего треугольника они все одинаковы.
| Желтый равносторонний треугольник с красный вписанный круг, фиолетовый описанный круг и зеленый ортокружность построены |
верх
Дроби и десятичные знаки
Какая часть площади этой фигуры зеленая?
Учащиеся используют модель площади для определения дроби.
Студенты могут:
- идентифицирует зеленый треугольник как единое целое, которое можно использовать для покрытия всей фигуры,
- подсчитать количество зеленых треугольников, необходимых для покрытия всей фигуры (55),
- назовите зеленый треугольник как единицу измерения (1/55),
- подсчитать общее количество зеленых насаждений, используя единицу измерения (например, 1/55, 2/55, 3/55,…, 10/55), и
- распознает, что этот счет дает правильную дробь (10/55 фигуры зеленого цвета).
Студентов также можно спросить:
- Желтая зона больше зеленой зоны?
- какая часть блоков зеленые? (модель набора)
- , чтобы создать форму, которая соответствует пяти шестым зеленым.
Примечание: Эта форма была создана с использованием файла образца динозавра и замены желто-коричневого ромба на красную трапецию, чтобы площадь можно было выразить в виде зеленого треугольника.
Именование дробей
| На рабочем столе щелкните изображение выше, чтобы открыть этот файл. | Ключ ответа |
Подобно тому, как учащиеся могут использовать реляционные стержни для сравнения различной длины, они могут использовать блоки шаблонов для сравнения областей различных форм с использованием дробей.
Этот пример можно изменить:
- замена шестиугольника на другую форму, состоящую из одного или нескольких блоков
- замена цифры «3» одним из других изображений в .zip-файле, созданном для этой цели, или любой дробной частью, нарисованной от руки
- с использованием различных форм в таблице
Студенты могли бросить вызов друг другу: «У меня две формы.Площадь одной формы составляет одну восьмую, а площадь другой формы — три четверти. Какими могут быть мои две формы? »
Или, для реальной задачи, используйте одну пятую и три четверти.
См. Задание «Изменение целого с помощью шаблонных блоков» в схемах обучения дробям.
Десятичные знаки
Блоки шаблонов + могут использоваться для представления десятичных знаков.
Представляет 1.8 более чем в одном направлении
Представьте и вычислите 0.5 ÷ 0,1
верх
Алгебра
Создавайте выражения и решайте уравнения.
Для набора треугольников общее количество сторон равно трехкратному количеству треугольников или s = 3 n .
Примечание: Это пример из математического ожидания 8-го класса — переменные, выражения и уравнения: перевод утверждений, описывающих математические отношения, в алгебраические выражения и уравнения.
Решите проблемы, связанные с шаблонными правилами.
PB Industries производит столы в форме лодок. Напишите выражение для количества мест, s , для t столов. Сколько столов нужно, чтобы разместить 100 человек?
Присваивайте значения различным блокам и придумывайте выражения, подставляйте значения в эти выражения и решайте уравнения, включающие эти выражения.
PB Industries создает выкройки из подручных материалов.
Он определяет, что его стоимость для создания блока шаблона составляет 0 долларов.05 за разрез.
Расставьте блоки от самых дешевых до самых дорогих.
Порядок первых четырнадцати блоков шаблона, показанный ниже, предполагает, что разрез сделан для каждой стороны блока.
Подрядчик решает выложить пол из блоков PB Industries.
Если подрядчик заботится только о покрытии по самой низкой цене, какие блоки следует использовать больше всего?
Учащийся может подумать, что блок с наибольшей площадью для каждой группы будет наиболее рентабельным, и затем отсортировать эти блоки от наиболее рентабельных к наименее рентабельным.
Для сравнения экономической эффективности этих шести блоков производится расчет ставки. Что означает коэффициент 0,05 для шестиугольника?
Расширения:
- Запишите зависимость между стоимостью и количеством резов в виде линейной функции. Постройте график этой функции. Создайте составную фигуру, которая будет стоить 1 доллар.
- Определите, как изменится ситуация, если материал будет стоить 0,12 доллара за кв. См, а самый маленький блок — это равносторонний треугольник с длиной стороны 1 см.
- Сравните стоимость различных рисунков плитки для комнаты размером 5 на 3 метра.
верх
Создайте контурный пазл
Создайте контурную головоломку или шаблон, аналогичный приведенному выше примеру с серой лодкой, а затем попросите других покрыть его шаблонными блоками (см. Связи с учебной программой 1-го класса [Ссылка № 2]).
Создание контурной головоломки с использованием математических шаблонных блоков + (PDF) описывает, как повернуть
блочная конструкция типа
в шаблон пазла, например
.
наверху
Файлы примеров
Чтобы получить доступ к образцу файла:
- щелкните ссылку в столбце Образец (только для ПК) или
- используйте кнопку «Открыть WWW» в диалоговом окне «Настройки» и укажите URL-адрес, или
- загрузите файл из столбца URL-адреса (щелкните правой кнопкой мыши и сохраните локально на рабочем столе, жестко коснитесь на мобильном устройстве) и используйте кнопку Открыть в инструменте, или
- добавить файлы примеров математики в папку Google Диска в «Мой диск», что обеспечивает удобный доступ на всех устройствах.
См. Страницу «Операции с файлами» для получения более подробной информации. Примечание: Эти файлы созданы для настольного компьютера и могут открываться не так, как показано на других устройствах.
top
Характеристики инструмента
верх
Прочие функции
Множественный выборЧтобы выделить блоки, обведите их рамкой. Щелкните блок, чтобы добавить или удалить его из выбора. Выбранные блоки можно перемещать, копировать, вращать, отражать по вертикали или горизонтали или повторно использовать как группу. | |
Настройка панели выбора Щелкните блок клонирования на панели выбора, чтобы изменить цвет всех блоков этого типа. |
верх
Сочетания клавиш
В настольной версии этого инструмента реализованы стандартные сочетания клавиш.
Ссылки
PDF поддерживает
- Основы математики — Пособие для учителя
- Ссылки на учебные планы блоков шаблонов
- Соединение фундаментальных математических концепций с mathies.ca (черновик)
- Создание контурной головоломки с использованием математических шаблонных блоков +
- mathies Инструменты и игры, используемые в WINS
- Шаблон блока шаблона
- Лист для манипуляций с блоками выкройки
(Источник — EduGAINS | Ресурсы, разработанные министерством | Математика | Уроки и поддержка | Манипуляторы)- Что такое блоки шаблона?
- Как блоки паттернов помогают учащимся?
- Примеры действий
- Рекомендуемые веб-сайты (датированные)
Посетите EduGAINS для получения дополнительных манипулятивных листов.
верх
70+ геометрических раскрасок для печати и настройки
Color with Fuzzy!
Я люблю создавать завораживающие геометрические раскраски со сложным дизайном. Теперь вы можете раскрасить более 70 цветов с этой страницы для взрослых и детей!
- математически точные двухмерные квадраты, круги, треугольники и звезды;
- 3D кубы, сферы, пирамиды и другие трехмерные фигуры;
- и кирпичные, завитые, мозаичные или черепичные узоры.
Прокрутите вниз, чтобы увидеть страну чудес геометрических форм и узоров!
~ Нечеткое
См. Ниже на этой странице
Простые геометрические раскраски
1. 3D геометрические раскраски
Распечатайте трехмерную геометрическую раскраску для создания трехмерного эффекта с различными иллюзиями.
Я могу получить небольшую комиссию через внешние ссылки. Как партнер Amazon я зарабатываю на соответствующих покупках.
Атрибуция: Многие изображения CWF лицензированы на GraphicsFactory.com.
Детям дошкольного и младшего школьного возраста понравятся раскраски без рекламы Fuzzy в формате PDF для печати . Они веселые
настроить и раскрасить для домашнего обучения.
Добавьте свое имя или напишите сообщение о дне рождения в своем
любимые шрифтов , РАЗМЕРЫ и цветов . Вам понравится использовать мои интерактивные раскраски для печати! См. Мою домашнюю страницу для получения дополнительной информации о цифровых загрузках.
- Используйте настройку буклета вашего принтера для поздравительных открыток .
- Используйте настройку кратных для печатных форм размером с куклу от двух до четырех.
- Детсадовцы любят это в школе и дома!
Также приготовьте ваши любимые мелки, цветные карандаши и акварели для моих расслабляющих раскрасок для взрослых!
~ Нечеткое
Я могу получить небольшую комиссию через внешние ссылки. Как партнер Amazon я зарабатываю на соответствующих покупках.
2. Раскраски с геометрическим рисунком звезд
Моя любимая геометрическая звезда — звезда компаса.Он настолько силен с морской точки зрения. Вы знаете кого-нибудь, кто является моряком или пилотом самолета? Раскрасьте компасную звезду как приятный сюрприз для этого особенного человека. Ищите оптические иллюзии.
3. Раскраски с квадратными и прямоугольными геометрическими фигурами
Эти раскраски имеют аккуратные квадратные и прямоугольные узоры. Помните: ромбы тоже часто рисуют в виде квадратов, особенно для выкройки лоскутного шитья.
Дамы любят создавать лоскутные одеяла и рисунки для других проектов.Вы можете увидеть ромб, крест и X на одном из этих лоскутных рисунков? Я думаю, это замечательно, как квадраты могут образовывать разные узоры. Некоторые из них также являются оптическими иллюзиями.
4. Круглые геометрические раскраски
Круглые геометрические раскраски могут быть такими витиеватыми. Мне нравятся круги, похожие на узоры спирографа, и я раскрашивал многие из них, когда был подростком.
Некоторые из этих картинок напоминают мне колеса обозрения, цветы и паутину.
Один выглядит как витраж со звездным рисунком, а другой — как солнечные лучи.
Детальные геометрические раскраски — PDF
5. Геометрическое сердце и геометрическая сова раскраски
Выберите одну из этих геометрических раскрасок совы, чтобы создать сложный или простой рисунок величественной совы.
- Еще у меня сердечек и сов побольше.
6. Геометрические стрекозы и бабочки Страницы
Бабочки и стрекозы добавляют фантазии этим геометрическим раскраскам.
7. Геометрические раскраски с орнаментом в виде листьев
Я люблю эти раскраски с геометрическими листьями. Лавровые венки напоминают мне победу в гонке. Мне больше всего нравится фигурный лист, потому что он такой необычный.
- Подумайте как о весенних, так и о осенних листьях. У меня здесь больше окраски листьев.
8. Цветочные геометрические раскраски
Эти геометрические раскраски цветов идеальны каждый раз!
9. Простая геометрия. Веселье
Конусы, кубы, пирамиды и сферы легко нарисовать линейкой и циркулем.Обучайте формы с помощью этих раскрасок по геометрии и узнавайте больше на моем сайте.
Еще бесплатные геометрические раскраски
У меня куча кельтских узоров для кельтского в глубине души, аккуратные кельтские узлы и узоры — даже трилистник, роза и чертополох или два. Мамам, папам и детям нравятся мои 3D-страницы, цветные рисунки и другие фигурные изображения:
Дети, взрослые и пожилые люди
Kids может раскрашивать их для координации глаз и рук.
Взрослые могут раскрашивать эти простыни для релаксации.
Модель для пожилых людей может использовать их, чтобы оставаться резкими, уделяя внимание деталям в рисунках и узорах. А все остальные могут раскрасить их в свое удовольствие!
Вы можете раскрасить их по временам года: красный и зеленый для Рождества, пастельные на Пасху и яркие цвета для весны и лета. Вы можете использовать весь спектр цветов радуги.
Спасибо за раскрашивание с помощью Fuzzy!
Детальные геометрические раскраски
исламских геометрических узоров — HiSoUR — Hi So You Are
🔊 Аудиочтение
В исламском декоре, где не используются образные изображения, часто используются геометрические узоры, выработанные веками.Художники исламского декора заменили диагноз, разработав узоры исламских геометрических узоров на протяжении веков. В исламском искусстве преобладали квадраты и круги, на которые можно было накладывать арабески, а также мозаики различных форм. Сложность и разнообразие стилей, используемых от звезд и простых вспомогательных средств в третьем веке хиджры до разнообразия от шести до тринадцати форм, были включены в седьмой век хиджры, за которыми следовали 14 и 16 звезд в десятом веке хиджры.Геометрические мотивы использовались в различных формах в исламском искусстве и архитектуре, включая персидские келим и жирафа, марокканскую плитку, перфорированную плитку, перфорированные окна с оврагами, керамику, кожу и витражи, изделия из дерева и металла.
Исламские геометрические формы были вдохновлены более простыми рисунками, использовавшимися в древнегреческой, римской и сасанидской цивилизациях. Геометрические мотивы представляют собой одну из трех форм исламского орнамента, в том числе гравюру с арабесками и арабскую каллиграфию; Геометрические мотивы и арабески — это формы взаимосвязанного искусства.
Геометрические узоры в исламском искусстве часто строятся на комбинациях повторяющихся квадратов и кругов, которые могут накладываться друг на друга и чередоваться, как и арабески (с которыми они часто комбинируются), образуя замысловатые и сложные узоры, включая большое количество мозаик. . Они могут составлять все украшение, могут образовывать основу для цветочных или каллиграфических украшений или могут уходить на задний план вокруг других мотивов. Сложность и разнообразие используемых узоров эволюционировали от простых звезд и ромбов в девятом веке до разнообразных узоров от 6 до 13 точек к 13 веку и, наконец, включили также 14- и 16-конечные звезды в шестнадцатом веке. .
Исламское искусство в основном избегает образных изображений, чтобы не становиться объектами поклонения. Исламские геометрические узоры произошли от более простых узоров, использовавшихся в более ранних культурах: греческой, римской и сасанидской. Это одна из трех форм исламского декора, другие — арабески, основанные на изогнутых и ветвящихся формах растений, и исламская каллиграфия; все три часто используются вместе. Геометрические узоры и арабески — это формы исламских узоров чередования.
Геометрические узоры встречаются в различных формах в исламском искусстве и архитектуре, включая ковры килим, персидский гирих и марокканскую плитку зеллидж, декоративные своды мукарнас, каменные ширмы с перфорацией джали, керамику, кожу, витражи, изделия из дерева и металла.
Генри Фусион говорит: «То, о чем я прошу, ничто не может лишить жизнь ее внешнего вида и передать ее скрытое содержание, такое как геометрические формы исламских мотивов. Эти образования — не что иное, как плод мысли, основанной на точном расчете, который может превратиться в своего рода график философских идей и духовных значений. Однако не следует забывать, что во время этого абстрактного кадра жизнь течет по линиям, образуя между ними образования, которые множатся и увеличиваются, спорадически и прерывисто, как будто существует непроницаемый дух, который смешивает эти образования и различает их, а затем собирает их снова.Интерпретация зависит от того, на что человек смотрит и на что надеется, и все они одновременно скрывают и раскрывают секрет потенциальной и безграничной энергии ». Кейт Кричлоу также утверждал, что исламские мотивы были созданы для того, чтобы привлечь наблюдателя к пониманию лежащих в основе истины, а не только для кажущегося украшения. «Большая часть исламского искусства, будь то архитектура, керамика, текстиль или книги, — это украшение», — сказал он. «Скрытая цель украшения — превратить мечети в легкое яркое тело, а украшение страниц Корана делает их вратами в бесконечность.Напротив, Дорис Бернс-Абу-Саиф в своей книге «Красота в арабской культуре» сказала, что существует большая разница между философским мышлением средневековой Европы и исламского мира, поскольку понятия красоты и качества в арабской культуре не совпадают. . Она также утверждала, что наслаждение красотой, будь то в поэзии или изобразительном искусстве, есть наслаждение самой красотой, без учета религиозных или психологических стандартов.
Авторы, такие как Кейт Кричлоу, утверждают, что исламские узоры созданы для того, чтобы привести зрителя к пониманию лежащей в основе реальности, а не просто для украшения, как иногда подразумевают авторы, интересующиеся только узором.Дэвид Уэйд утверждает, что «большая часть искусства ислама, будь то архитектура, керамика, текстиль или книги, — это искусство украшения, то есть преображения». Уэйд утверждает, что цель состоит в том, чтобы преобразить, превратив мечети «в легкость и узор», в то время как «украшенные страницы Корана могут стать окнами в бесконечность». Напротив, Дорис Беренс-Абусейф в своей книге «Красота в арабской культуре» заявляет, что «основное различие» между философским мышлением средневековой Европы и исламского мира состоит именно в том, что в арабской культуре понятия добра и прекрасного разделены.Она утверждает, что красотой, будь то в поэзии или в изобразительном искусстве, наслаждались «ради нее самой, без привязки к религиозным или моральным критериям».
Многие исламские узоры построены на квадратах и кругах, которые обычно повторяются, перекрываются и переплетаются, образуя замысловатые и сложные узоры. Повторяющийся мотив — восьмиконечная звезда, часто встречающаяся в исламской плитке; он состоит из двух квадратов, один из которых повернут на 45 градусов относительно другого. Четвертая основная форма — многоугольник, включающий пятиугольники и восьмиугольники.Все это можно комбинировать и переделывать, чтобы сформировать сложные узоры с множеством симметрий, включая отражения и вращения. Такие шаблоны можно рассматривать как математические мозаики, которые могут продолжаться бесконечно и, таким образом, предполагать бесконечность. Они построены на сетках, для рисования которых требуется только линейка и циркуль. Художник и педагог Роман Веростко утверждает, что такие конструкции на самом деле являются алгоритмами, что делает исламские геометрические узоры предшественниками современного алгоритмического искусства.
Круг символизирует единство и разнообразие природы, и многие исламские узоры начинаются с круга.Например, украшение мечети 15-го века в Йезде, Иран, основано на круге, разделенном на шесть на шесть окружностей, начерченных вокруг него, все соприкасаются в его центре и каждый касается центров двух своих соседей, образуя правильный шестиугольник. На этой основе построена шестиконечная звезда, окруженная шестью меньшими неправильными шестиугольниками, чтобы сформировать мозаичный узор звезды. Это составляет основной дизайн, который выделяется белым цветом на стене мечети. Однако этот рисунок покрыт пересекающимся узором синего цвета вокруг плиток других цветов, образуя сложный узор, который частично скрывает исходный и лежащий в основе дизайн.Подобный дизайн образует логотип Исследовательского центра Мохаммеда Али.
Эрнест Ханбери Ханкин, один из первых западных исследователей исламских узоров, определил «геометрическую арабеску» как узор, образованный «с помощью линий построения, состоящих из соприкасающихся многоугольников». Он заметил, что можно использовать множество различных комбинаций многоугольников, если остаточные пространства между многоугольниками достаточно симметричны. Например, сетка контактирующих восьмиугольников имеет квадраты (с той же стороны, что и восьмиугольники) в качестве остаточных пространств.Как видно из гробницы Акбара, Сикандра (1605–1613 гг.), Каждый восьмиугольник является основой 8-конечной звезды. Ханкин считал «умение арабских художников находить подходящие комбинации многоугольников… почти поразительным». Далее он отмечает, что если в углу появляется звезда, должна быть показана ровно одна ее четверть; если по краю — ровно его половину.
Свиток Топкапы, изготовленный в Иране при династии Тимуридов в конце 15-го или начале 16-го века, содержит 114 узоров, включая цветные рисунки для плиток гирих и квартала или полукупола мукарна.
Математические свойства декоративной плитки и лепных украшений дворца Альгамбра в Гранаде, Испания, были тщательно изучены. Некоторые авторы утверждали на сомнительных основаниях, что нашли там большую часть или все 17 групп обоев. Марокканские геометрические изделия из дерева с 14 по 19 века используют только 5 групп обоев, в основном p4mm и c2mm, иногда p6mm и p2mm, а реже p4gm; Утверждается, что метод построения «Hasba» (мера), который начинается с n-кратных розеток, может, однако, генерировать все 17 групп.
Круги сыграли важную роль в структуре этих мотивов, и дизайнеры использовали их для использования линейки и штангенциркуля. Многие геометрические формы, такие как револьвер, восьмиугольник, треугольник, квадрат и пентакль, были созданы путем регулярного повторения, перекрытия и переплетения квадратов и кругов в сложных узорах, заполняя некоторые пространства и оставляя некоторые пустыми. это от части к части. Восемь звезд часто использовались в исламской плитке и обычно состояли из двух квадратов, один из которых был под углом 45 градусов к другому.Также использовались другие многоугольники, такие как сквош и восьмиугольник. Эти формы можно комбинировать для образования сложных узоров с помощью различных форм симметрии, таких как отражение и вращение. Эти геометрические узоры можно рассматривать как геометрическую мозаику, которая может растягиваться бесконечно. Художник Роман Верстико утверждает, что эти формы на самом деле являются алгоритмами, что делает исламские геометрические конструкции предшественниками искусства современных алгоритмов. В своей книге «Инженерные концепции в исламском искусстве» Эссам аль-Сайид и Аиша Барман объяснили, что мусульманские декораторы использовали систему, в которой инженерные сети были разделены на идентичные блоки, которые повторялись на регулярной основе.Это делается путем деления площади на квадраты или пистолеты одинакового размера, вычерчивая внутри каждого юнита геометрическую форму, которая берется за основу сетки, на которой будет построена схема этого юнита. Каждая единица каждого объекта связана с другими подобными единицами, чтобы составить общую форму этой области. Этот метод помогал легко увеличивать и минимизировать декоративные рисунки, основываясь на относительных отношениях между геометрическими формами.
Например, украшения мечети в Йезде в Иране содержат главный круг, разделенный на шесть кругов с шестью частями, каждая из которых проходит через центр соседних кругов, образуя шестиугольник.Таким образом, шестиугольные звезды были сформированы из меньших, неправильных пистолетов, и весь дизайн образует мозаичный мотив. Исследовательский центр Мохаммеда Али принял аналогичный дизайн. Эрнест Ханбери Ханкин, один из первых исследователей исламского орнамента арабески, описал его как украшение, сформированное с использованием базовых линий, образовавшихся в результате соприкосновения многоугольников. Ханкин отметил, что комбинация многоугольников может использоваться, если оставшиеся промежутки между многоугольниками симметричны. Например, при сетевом подключении оценщиков будут прямоугольники в промежутках между восьмиугольниками.
Самыми ранними геометрическими формами в исламском искусстве были отдельные отдельные геометрические формы, такие как восьмиконечные звезды и ромбики, содержащие квадраты. Они датируются 836 годом в Великой мечети Кайруана, Тунис, и с тех пор распространились по всему исламскому миру.
Следующим этапом развития, ознаменовавшим средний этап использования исламского геометрического узора, стали 6- и 8-конечные звезды, которые появились в 879 году в мечети Ибн Тулуна в Каире, а затем получили широкое распространение.
С 11 века использовалось более широкое разнообразие узоров.Абстрактные 6- и 8-точечные формы появляются в Башне Харакана в Казвине, Персия, в 1067 году, и в мечети Аль-Джуюши, Египет, в 1085 году, и снова становятся широко распространенными оттуда, хотя 6-точечные узоры редко встречаются в Турции.
В 1086 году в Пятничной мечети в Исфахане появляются 7- и 10-угольные узоры гирих (с семиугольниками, 5- и 6-конечными звездами, треугольниками и неправильными шестиугольниками). 10-балльный гирих получил широкое распространение в исламском мире, за исключением испанского Аль-Андалуса. Вскоре после этого широкие 9-, 11- и 13-точечные узоры гирих были использованы в мечети Барсиан, также в Персии, в 1098 году; они, как и геометрические узоры из семи точек, редко используются за пределами Персии и Центральной Азии.
Наконец, знаменуя конец средней стадии, 8- и 12-точечные узоры гирих-розеток появляются в мечети Алаэддин в Конье, Турция в 1220 году, и во дворце Аббасидов в Багдаде в 1230 году, получив широкое распространение в исламских странах. Мир.
Начало поздней стадии ознаменовано использованием простых 16-точечных узоров в мавзолее Хасана Садака в Каире в 1321 году и в Альгамбре в Испании в 1338–1390 годах. Эти закономерности редко встречаются за пределами этих двух регионов.Более сложные комбинированные 16-точечные геометрические узоры встречаются в комплексе султана Хасана в Каире в 1363 году, но редко где-либо еще. Наконец, 14-точечные узоры появляются в Джама Масджид в Фатехпур-Сикри в Индии в 1571–1596 годах, но в нескольких других местах.
Художественные формы:
В нескольких художественных формах в разных частях исламского мира используются геометрические узоры. К ним относятся керамика, гирих, каменные ширмы с пирсингом джали, коврики килим, кожа, изделия из металла, своды мукарнас, витражи шакаба, изделия из дерева и плитка зеллиге.
В керамике можно использовать круговые мотивы, как радиальные, так и тангенциальные. Миски или тарелки можно украсить изнутри или снаружи радиальными полосами; они могут быть частично образными, представлять собой стилизованные листья или лепестки цветов, в то время как круглые полосы могут проходить вокруг чаши или кувшина. Узоры этого типа использовались на исламской керамике периода Айюбидов 13 века. Радиально-симметричные цветы, скажем, с 6 лепестками поддаются все более стилизованному геометрическому рисунку, который может сочетать геометрическую простоту с узнаваемыми натуралистическими мотивами, яркой глазурью и радиальной композицией, которая идеально подходит для круглой посуды.Гончары часто выбирали узоры, подходящие к форме изготавливаемого ими сосуда. Так, глиняная неглазурованная фляга для воды из Алеппо в форме вертикального круга (с ручками и горлышком наверху) украшена кольцом лепного плетения вокруг арабской надписи с маленьким восьмилепестковым цветком в центре.
Гирих — это сложные узоры переплетения, состоящие из пяти стандартных форм. Этот стиль используется в персидской исламской архитектуре, а также в декоративных изделиях из дерева. Дизайны Girih традиционно выполняются в различных материалах, включая резаную кирпичную кладку, лепнину и мозаичную фаянсовую плитку.В изделиях из дерева, особенно в период Сефевидов, он мог применяться либо в виде решетчатых рам, либо оставленных гладкими, либо вставленных с панелями, например, из цветного стекла; или как мозаичные панели, используемые для украшения стен и потолков, священных или светских. В архитектуре гирих образует декоративные переплетенные ленточные поверхности с 15 по 20 век. Большинство дизайнов основаны на частично скрытой геометрической сетке, которая обеспечивает регулярный массив точек; это превращается в узор с использованием 2-, 3-, 4- и 6-кратной симметрии вращения, которая может заполнять плоскость.Видимый узор, наложенный на сетку, также является геометрическим, с 6-, 8-, 10- и 12-конечными звездами и множеством выпуклых многоугольников, соединенных ремнями, которые обычно переплетаются друг с другом. Видимый узор не совпадает с лежащей под ним плиткой.
Джали — это перфорированные каменные ширмы с регулярно повторяющимся узором. Они характерны для индо-исламской архитектуры, например, в зданиях династии Великих Моголов в Фатехпур-Сикри и Тадж-Махале. Геометрические узоры сочетают в себе многоугольники, такие как восьмиугольники и пятиугольники, с другими формами, такими как 5- и 8-конечные звезды.Узоры подчеркивали симметрию и предполагали бесконечность повторением. Джали служил окнами или перегородками, обеспечивая уединение, но пропускал воздух и свет. Джали является выдающимся элементом архитектуры Индии. Использование перфорированных стен уменьшилось в связи с современными строительными стандартами и необходимостью обеспечения безопасности. Современные, упрощенные стены джали, например, сделанные из предварительно формованных глиняных или цементных блоков, были популяризированы архитектором Лори Бейкер. Пробитые окна в стиле гирих иногда встречаются в других частях исламского мира, например, в окнах мечети Ибн Тулуна в Каире.
Килим — исламский плоский тканый ковер (без ворса), предназначенный для домашнего использования или молитвенный коврик. Узор создается путем наматывания уточных нитей на нити основы при достижении границы цвета. Эта техника оставляет зазор или вертикальную щель, поэтому килимы иногда называют тканью с щелевой тканью. Килимы часто украшают геометрическими узорами с 2- или 4-кратной зеркальной или вращательной симметрией. Поскольку в ткачестве используются вертикальные и горизонтальные нити, изгибы трудно создавать, и поэтому рисунки формируются в основном с прямыми краями.Узоры килим часто характерны для конкретных регионов. Мотивы килим часто бывают как символическими, так и декоративными. Например, волчья пасть или волчья лапка (турецкий: Kurt Aǧzi, Kurt İzi) выражают желание племенных ткачей защитить стада своих семей от волков.
Исламская кожа часто имеет тиснение с узорами, аналогичными уже описанным. Кожаные обложки для книг, начиная с Корана, где фигуративные произведения искусства были исключены, были украшены комбинацией куфического письма, медальонов и геометрических узоров, обычно окаймленных геометрической тесьмой.
Металлические артефакты имеют те же геометрические узоры, что и в других формах исламского искусства. Однако, по мнению Гамильтона Гибба, акценты различны: геометрические узоры, как правило, используются для границ, а если они находятся в основной декоративной области, они чаще всего используются в сочетании с другими мотивами, такими как цветочные узоры, арабески, животные мотивы. , или каллиграфическим шрифтом. Геометрические узоры в исламских металлических изделиях могут образовывать сетку, украшенную этими другими мотивами, или они могут формировать фоновый узор.
Даже там, где металлические предметы, такие как миски и тарелки, кажется, не имеют геометрического орнамента, все же узоры, такие как арабески, часто располагаются в восьмиугольных отсеках или располагаются концентрическими полосами вокруг предмета. Используются как закрытые рисунки (которые не повторяются), так и открытые или повторяющиеся рисунки. Такие узоры, как переплетенные шестиконечные звезды, были особенно популярны с 12 века. Ева Баер отмечает, что, хотя этот дизайн был по сути прост, он был разработан мастерами по металлу в замысловатые узоры, переплетенные арабесками, иногда организованные вокруг других основных исламских узоров, таких как шестиугольный узор из шести перекрывающихся кругов.
Мукарны — это искусно вырезанные потолки к полукуполам, часто используемые в мечетях. Обычно они изготавливаются из лепнины (и, следовательно, не имеют структурной функции), но также могут быть из дерева, кирпича и камня. Они характерны для исламской архитектуры средневековья от Испании и Марокко на западе до Персии на востоке. Архитектурно они образуют несколько ярусов скребков, уменьшающихся в размерах по мере подъема. Часто их украшают искусно.
Витражи с геометрическим рисунком используются в различных интерьерах исламской архитектуры.Он находится в сохранившейся летней резиденции Дворца Шекинских ханов в Азербайджане, построенной в 1797 году. Узоры на окнах «шабака» включают 6-, 8- и 12-конечные звезды. Эти декоративные окна с деревянными рамами являются отличительной чертой дворцовой архитектуры. Шабаки по-прежнему строятся традиционным способом в Шеки в 21 веке. Традиции витражей в деревянных рамах (не свинцовых, как в Европе) сохранились в мастерских как в Иране, так и в Азербайджане. Застекленные окна, оформленные лепным орнаментом в виде гирих, встречаются как в Турции, так и в арабских странах; поздний образец без традиционного баланса элементов дизайна был сделан в Тунисе для Международной колониальной выставки в Амстердаме в 1883 году.В старом городе Сана в Йемене в высоких зданиях витражи.
Zellige — это глазурованные терракотовые плитки, вставленные в штукатурку, образующие красочные мозаичные узоры, включая регулярную и полурегулярную мозаику. Традиция характерна для Марокко, но также встречается в мавританской Испании. Зеллиге используют для украшения мечетей, общественных зданий и богатых частных домов.
Интерес к исламским геометрическим узорам растет на Западе, как среди мастеров, так и среди художников, включая М.C. Escher в двадцатом веке, и среди математиков и физиков в тех числе Питера Дж Л и Пол Стейнхардт, который спорно утверждал, что в 2007 году тайлинги в то Дарб-е Имамы святыня в Исфахане может генерировать квазипериодические модели как Пенроуз паркеты.
В западном обществе иногда предполагают, что ошибки в повторяющихся исламских узорах, например, на коврах, были намеренно введены как проявление смирения художниками, которые верили, что только Аллах может создать совершенство, но эта теория отрицается.
В крупных западных коллекциях хранится множество предметов из самых разных материалов с исламскими геометрическими узорами. В Музее Виктории и Альберта в Лондоне хранится не менее 283 таких предметов из материалов, включая обои, резное дерево, инкрустированное дерево, глиняную посуду с оловянным или свинцовым покрытием, латунь, лепнину, стекло, тканый шелк, слоновую кость, а также рисунки пером или карандашом. В Метрополитен-музее в Нью-Йорке есть среди других соответствующих коллекций 124 средневековых (1000–1400 гг. Н. Э.) Предметов с исламскими геометрическими узорами, включая пару египетских дверей минбара (кафедры) почти 2 метра.с высоким содержанием палисандра и тутового дерева, инкрустированные слоновой костью и черным деревом; и целый михраб (молитвенная ниша) из Исфахана, украшенный полихромной мозаикой и весом более 2000 кг.
Голландский художник М. К. Эшер был вдохновлен замысловатыми декоративными узорами Альгамбры для изучения математики мозаики, что изменило его стиль и повлияло на всю его творческую карьеру. По его собственным словам, это был «самый богатый источник вдохновения, к которому я когда-либо обращался».
Культурные организации, такие как Институт математических наук и Институт перспективных исследований, проводят мероприятия, посвященные геометрическим узорам и связанным с ними аспектам исламского искусства.В 2013 году Стамбульский центр дизайна и фонд Ensar провели в Стамбуле, как они утверждали, первый симпозиум исламского искусства и геометрических узоров. В состав группы вошли эксперты по исламскому геометрическому узору Кэрол Бир, Джей Боннер, Эрик Броуг, Хакали Нечефоглу и Реза Сарханги. В Великобритании Школа традиционных искусств принца проводит ряд курсов по исламскому искусству, включая геометрию, каллиграфию и арабески (растительные формы), изготовление плитки и резьбу по гипсу.
Компьютерная графика и автоматизированное производство позволяют эффективно и экономично разрабатывать и производить исламские геометрические узоры.Крейг С. Каплан объясняет и иллюстрирует в своей докторской диссертации. тезис о том, как алгоритмически генерировать исламские звездные узоры
Два физика, Питер Дж. Лу и Пол Стейнхардт, вызвали разногласия в 2007 году, заявив, что конструкции гириха, подобные тому, что использовалась в святилище Дарб-е Имам в Исфахане, могли создавать квазипериодические мозаики, похожие на те, что были обнаружены Роджером Пенроузом в 1973 году. Они показали, что вместо традиционной линейки и компаса можно создавать рисунки гирих, используя набор из пяти «плиток гирих», все равносторонние многоугольники, вторично украшенные линиями (для ремня).
В 2016 году Ахмад Рафсанджани описал использование исламских геометрических узоров на башнях гробниц в Иране для создания ауксетических материалов из перфорированных резиновых листов. Они стабильны как в сжатом, так и в расширенном состоянии и могут переключаться между ними, что может быть полезно для хирургических стентов или компонентов космического корабля. Когда обычный материал растягивается вдоль одной оси, он сжимается вдоль других осей (под прямым углом к растяжению). Но ауксетические материалы расширяются под прямым углом к растяжению.Внутренняя структура, которая обеспечивает такое необычное поведение, вдохновлена двумя из 70 исламских узоров, которые Рафсанджани отметил на башнях гробниц.
| Искусство и геометрия | ||||
Что такое искусство? Что ж, у каждого, кто задавал этот вопрос, был бы другой ответ, потому что у всех нас разные симпатии и антипатии. Каждая культура мира оценивает искусство и то, как оно эстетически соотносится с их окружением и / или верованиями.Эстетическое понимание произведения искусства — это сочетание способности видеть, интерпретировать и оценивать его. Следовательно, у одного человека может быть другая точка зрения на произведение искусства, чем у представителя другой культуры. В истории греки считались высшей культурой. Однако Уильям М. Айвинс-младший изучал искусство греков, а также их геометрию. В своей книге «Искусство и геометрия: исследование пространственной интуиции» Айвинс проводит противоречивое исследование вышеупомянутого мифа.По словам Ивинса, греки обладали «осязательным умом», что означает, что они создавали произведения искусства, которые воспринимались через осязание. «Тактильное» мировоззрение греков проявляется в их искусстве в отсутствии движения, эмоциональных и духовных качеств. Ивинс продолжает, что искусство греков возникло в результате неполного понимания законов перспективы. Итак, что подразумевается под «законами перспективы»? Проще говоря, это означает правильную технику для представления трехмерного объекта на двухмерной поверхности. Художники эпохи Возрождения первыми преуспели в перспективе. В 1636 году человек по имени Жирар Дезарг представил свою «перспективную лестницу». Художники использовали это как инструмент для привнесения перспективы в свою работу. Подобно тому, как греки основывали свое искусство на осязательных качествах, они не ушли далеко от этого образа мысли в своей геометрии. Они считали, что параллельные линии остаются параллельными навсегда. Таким образом, отсутствие у них современной мысли о геометрической непрерывности и перспективе поставило греков в невыгодное положение в математической области.Геометрия прогрессировала во времени и включала в себя перспективную геометрию. Ниже приведен пример разделителя строк. Это помогает привнести перспективу в линейный дизайн и оптическое искусство, в котором используется геометрия. Сегодня художники часто используют геометрические элементы, такие как линии, углы и формы, для создания темы во всех своих произведениях. Также художники начали использовать эти геометрические элементы как способ создания иллюзии третьего измерения. Это искусство известно как оптическое или оптическое искусство. Ниже приводится пример оптического искусства. Студенты должны начать изучение оптического искусства с создания линейных рисунков и работы с симметрией. См. Пример дизайна линий ниже. Затем учащиеся могут применить концепцию затенения к своим проектам, чтобы создать ощущение перспективы. Студенты будут развивать свой пространственный интеллект для понимания продвинутой математики. | ||||
| Предоставлено Ланеттой Дж. Бёрдетт | ||||
Ссылка: Айвинс-младший, W.M. «Искусство и геометрия: исследование пространственной интуиции» (1946) Dover Publications, Inc. Нью-Йорк: Нью-Йорк. Сеймур, Д., Силви, Л. и Снайдер, Дж. «Конструкции линий» (1994). Идеальная компания по снабжению школ. Алсип, Иллинойс. Томпсон, К. и Лофтус, Д. «Связи искусства: интеграция искусства в учебную программу» (1995) Good Year Books. Гленвью, Иллинойс. | ||||
| Содержание | Далее | ||||
| Лента Мебиуса | ||||
Биографическая информация Август Фердинанд Мебиус родился в 1790 году в Саксонии (ныне Германия), Лента Мебиуса Мебиус был пионером в области топологии. Топология — это исследование Мебиус предположил, что многогранник представляет собой совокупность соединенных Чтобы просмотреть несколько различных примеров, | ||||
| Предоставлено Стивом Бикслером | ||||
Рекомендации:
| ||||
| Содержание | Далее | Назад | ||||
| Формула Эйлера | ||||
В середине девятнадцатого века новое развитие геометрии под названием топология начало обретать форму (это не каламбур!).Топология — это изучение геометрических фигур, которое сохраняется даже тогда, когда фигуры подвергаются изменениям таким образом, что их свойства теряются. Несколько отдельных открытий, сделанных до середины девятнадцатого века, стали известны в ходе современного развития топологии. Одна из самых важных — это формула, показывающая отношения между вершинами, ребрами и гранями простых многогранников. Обобщения, которые стали известны как «формула Эйлера», занимают свое место среди центральных теорий геометрии. Формула Эйлера — одна из самых важных теорем геометрии, с пятнадцатью различными доказательствами, появившимися с момента ее создания, впервые открытая Декартом, а затем переоткрытая Эйлером, которому мы приписываем эту теорему, в 1752 году. Показывает связь между вершинами, гранями и ребрами. простых многогранников Эйлер интересовался классификацией многогранников. Эйлер представляет свою теорему как число вершин плюс число граней минус число ребер любого простого многогранника будет равно двум; V + F — E = 2 .На основании его результатов было определено, что существует только пять платоновых тел, которые можно построить, выбрав правильный многоугольник и имея одинаковое количество форм, пересекающихся в каждом углу. Пять Платоновых Тел включают: Можете ли вы удовлетворить формулу Эйлера для вышеуказанных геометрических фигур? Куб, например, имеет восемь вершин, шесть граней и двенадцать ребер или 8 + 6 — 12 = 2. Все пять этих форм можно найти в природе. Куб, тетраэдр и октаэдр можно найти в кристаллах, а додекаэдр и икосаэдр можно найти в некоторых вирусах и радиоилляриях.Это был бы прекрасный способ объединить математику с наукой. | ||||
| Предоставлено Яном Свенсоном | ||||
Рекомендации:
| ||||
| Содержание | Далее | Предыдущие | ||||
| Танграммы | ||||
Что такое Танграм? Вот выкройка для изготовления деталей танграма. Какова история Tangram? Танграм сегодня.. . Правила пазла: Вот несколько головоломок, которые стоит попробовать: | ||||
| Предоставлено Анжелой Церадски | ||||
Рекомендации:
| ||||
| Содержание | Далее | Предыдущее | ||||
| Тесселяция | ||||
Вы когда-нибудь хотели создать произведение искусства, но не знали, с чего начать? Подумайте, какие отношения существуют между искусством и математикой.Художники используют математику по-разному. Приведу несколько примеров. Искусство, изображающее высоту и ширину, представляет собой двухмерный дизайн. Трехмерное искусство показывает высоту, ширину и глубину. Искусство также использует пропорции, узоры и геометрию. Пропорция — это отношение части к целому или к другой части. Узорчатка играет большую роль в развитии искусства. В следующий раз, когда вы пойдете в художественный музей, внимательно посмотрите на произведения и попытайтесь найти закономерности и математическое влияние. Повторение узора называется тесселяцией.M.C. Эшер, известный художник, использовал концепцию мозаики во многих своих работах. Концепция тесселяции состоит из перерисовки формы с помощью скольжения, отражения (переворота) и поворота (поворота). Точка, в которой три или более плитки встречаются в мозаике, называется вершиной. Треугольники, квадраты и шестиугольники — это правильные многоугольники, которые сами по себе мозаичны. Это можно доказать математически. Полный оборот составляет 360 o . Используя равносторонний треугольник с углами 60 o , 6 (60 o ) = 360 o .Этот расчет доказывает, что шесть плиток встречаются в вершине мозаики плитки. Четыре плитки встречаются в вершине квадрата; 4 (90 o ) = 360 o . Шестиугольник с углами 120 градусов имеет три плитки, которые встречаются в вершине; 3 (120 o ) = 360 o . Для создания мозаики таких многоугольников, как пятиугольник, семиугольник и восьмиугольник, можно использовать различные типы правильных многоугольников. Для мозаики выберите одну или две геометрические фигуры. Создайте мозаику, сдвигая, отражая или вращая фигуру.После создания узора или рисунка добавьте к формам цвет и текстуру. Картина представляет собой произведение искусства с математической основой. Можно ли изменить узор, изменив внешний вид формы или форм? Попробуйте создать другой вид, используя ту же геометрическую форму или формы с небольшими вариациями, и увидите разницу в конечном результате. Исследование тесселяции может быть очень захватывающим. Ниже приведена иллюстрация, демонстрирующая тесселяцию.Три простые формы показывают методы слайда , отражения (переворот) и вращения (поворот). В целях объяснения начните со средней плитки. Метод slide используется для перерисовки средней плитки на плитку над ней. Сверху плитка воспроизводится по часовой стрелке с использованием методов отражения , слайда , отражения и поворота последовательно. | ||||
| Предоставлено CiCi Naifeh | ||||
Рекомендации:
| ||||
| Содержание | Далее | Назад | ||||
| Многогранник | ||||
Многогранник — это геометрическая фигура, которая является трехмерной версией плоского многоугольника.Другими словами, это конечный связный набор многоугольников, соединенных вместе таким образом, что каждая сторона каждого многоугольника совпадает (соединяется) со стороной ровно одного другого многоугольника. Изучение многогранников было популярным предметом изучения греческой геометрии еще до Платона (427 — 347 до н. Э.). В 1640 году французский философ, математик и ученый Рене Декарт обнаружил следующую формулу. В 1752 году швейцарский математик Леонард Эйлер заново открыл и использовал его.
Эта формула верна для простых многогранников . Многогранник называется простым , если в нем нет отверстий; то есть поверхность может непрерывно деформироваться в поверхность сферы.Есть более сложные, у которых есть свои формулы. В общем, простые многогранники делятся на две категории: выпуклые и вогнутые. Выпуклый многогранник определяется следующим образом: ни один отрезок прямой, соединяющий две его точки, не содержит точки, принадлежащей его внешней стороне. С другой стороны, вогнутый многогранник будет иметь отрезки прямых, которые соединяют две его точки со всеми точками, кроме двух, лежащих снаружи. Ниже приведен пример вогнутого многогранника. Наиболее интересными являются правильные многогранники .В правильном многограннике все грани — правильные многоугольники, которые конгруэнтны. Кроме того, все вершины правильного многогранника лежат на поверхности сферы. Как оказалось, существует всего пять правильных многогранников, и их часто называют платоновыми телами . | ||||
| Предоставлено Сьюзан Истман | ||||
Рекомендации:
| ||||
| Содержание | Далее | Назад | ||||
Топ-10 закономерностей, встречающихся в природе | Fibonacci serie
Природа — из-за огромного разнообразия форм и структуры всегда была вдохновляющей музой множества писателей, художников и поэтов.Что, возможно, менее известно, так это то, что это огромное разнообразие форм и структур очень удивляло, заинтриговало и взволновало большое количество математиков, которые всегда пытались найти закономерности в огромном разнообразии природных узоров, чтобы разгадать их загадки. Чтобы оценить, может ли механизм настройки действительно рассматриваться как общий основной процесс, способствующий формированию паттернов в физике, химии и биологии, настоятельно требуется методологический сдвиг в обычном способе использования математики, при этом различная роль, которую играют химия и биология, особенно поучительна. .
1. Узоры на листьях —
Живой мир наполнен полосами и линьками контрастных цветов со скульптурными эквивалентами тех, что реализованы в виде гребней и впадин на поверхности; с моделями организации и поведения даже среди отдельных организмов. Людей уже давно искушает найти какой-то неясный «разум» за всеми этими биологическими паттернами. Эван еще в начале 20 века, бельгийский символист Морис Метерликнк, размышлял об эффективной организации пчелиных и термитных колоний.
Образец листьев — это образец или метод, с помощью которого листья прикрепляются к веткам и стеблям. Ботаники обычно различают три основных типа листьев: чередующиеся, супротивные и мутовчатые. Расположение жилок на листе называется рисунком жилкования; Однодольные имеют параллельное жилкование, а двудольные — сетчатое. … В расположении противоположных листьев два листа соединяются в узле. В мутовчатом расположении три или более листа соединяются в узел.
Тип жилкования листа подразделяется на сетчатый, параллельный или дихотомический.В сетчатом жилковании жилки расположены в виде сетки, в том смысле, что все они связаны между собой, как нити сети. При параллельном жилковании все жилки меньше по размеру и параллельны или почти параллельны друг другу, хотя ряд более мелких жилок соединяет большие жилки. Параллельное жилкование встречается на листьях почти всех однодольных покрытосеменных, зародыши которых имеют одну семядоль, как у цветковых растений, таких как лилии и травы.
2. Спиральный узор —
Nautilus — еще один кропотливый мастер, который проектирует свою раковину в форме, называемой логарифмической или равноугольной спиралью (объяснение ниже).Эта точная кривая развивается естественным образом по мере увеличения раковины, но не меняет своей формы, постоянно растет, но никогда не меняет своих пропорций. Процесс самоподобного роста дает логарифмическую спираль. Мы находим ту же спираль в рогах горного барана и на пути, проложенном мотыльком, направленным к свету. Для математически наклонных людей такую кривую можно кратко описать формулой R = C * (Ang), где R — радиус кривой, C — постоянная величина и (Ang) — угол, на который кривая имеет вращался.Это может дополнительно подтвердить ряд Фибоначчи.
Последовательность Фибоначчи демонстрирует определенный числовой паттерн, который возник как ответ на упражнение в первом школьном учебнике алгебры. Оказалось, что этот паттерн имеет гораздо больший интерес и важность, чем предполагал его создатель. Его можно использовать для моделирования или описания удивительного разнообразия явлений в математике и естественных науках, искусстве и природе. Математические идеи, к которым приводит последовательность Фибоначчи, такие как золотое сечение, спирали и самоподобные кривые, давно ценились за их очарование и красоту, но никто не может толком объяснить, почему они так ясно отражаются в мире искусства и искусства. природа.
Еще более захватывающим является удивительное появление чисел Фибоначчи и их относительных соотношений в областях, далеких от логической структуры математики: в природе и искусстве, в классических теориях красоты и пропорций.
Рассмотрим простейший пример геометрического роста — бесполое размножение, как у амебы. Каждый организм разделяется на два по истечении периода времени созревания, характерного для данного вида. Этот интервал варьируется случайным образом, но в определенном диапазоне в зависимости от внешних условий, таких как температура, наличие питательных веществ и так далее.Мы можем представить себе упрощенную модель, в которой в идеальных условиях все амебы разделяются после одного и того же периода роста. Получаем последовательность удвоения. Обратите внимание на рекурсивную формулу:
An = 2An
3. Узор на полосках зебры —
Подумайте о поразительной регулярности чередования темных и светлых полос на шерсти зебры или сетчатости на поверхности плодов. тело сморчка (разновидность гриба) гриба.Увеличивая изображение слизистой плесени, вы можете наблюдать паттерны разветвленной сети, которые появляются по мере роста плесени. В еще меньшем масштабе, увеличенном в несколько сотен раз, похожие узоры появляются на поверхности пыльцевого зерна.
Шерсть зебры чередуется контрастными участками светлой и темной пигментации. На техническом жаргоне пигментация отражает паттерны активации и торможения — подходящие термины из-за динамического процесса, который порождает паттерн. Клетки кожи, называемые меланоцитами, производят пигменты меланина, которые передаются в растущие волосы зебры.Производит ли меланоциты свой пигмент, по-видимому, определяется наличием или отсутствием определенных химических активаторов в коже во время раннего эмбрионального развития. Следовательно, рисунок шерсти зебры отражает раннее взаимодействие этих химических веществ, когда они проникали через кожу зародыша. С новым набором правил двумерный клеточный автомат может легко стимулировать узор шерсти и, таким образом, пролить свет на механизм формирования узора у зебры. Вернитесь к квадратной сетке и случайным образом разместите черную или белую ячейку на каждом квадрате.Сетка будет выглядеть примерно так, как крайняя левая рамка на рисунке 3. Предположим, что каждая черная ячейка представляет определенный минимальный уровень активатора пигмента. Такой случайный набор активатора или его отсутствие считается отправной точкой раннего развития рисунка шерсти.
4. Узор, найденный в сотах —
Некоторые узоры вылеплены со строгой регулярностью. По крайней мере, на первый взгляд, происхождение регулярных паттернов часто кажется легко объяснимым. Ячейки соты тысячи раз повторяют свою гексагональную симметрию.Пчела — опытный и неутомимый ремесленник с врожденной способностью измерять ширину и толщину сот, которые она строит. Хотя работа разума насекомого может сбивать с толку биологов, регулярность сот свидетельствует об удивительных архитектурных способностях медоносной пчелы.
Оси сотовых ячеек всегда квазигоризонтальны, а несвязанные ряды сотовых ячеек всегда выровнены по горизонтали (а не по вертикали). Таким образом, каждая ячейка имеет две вертикально ориентированные стенки, причем верхняя и нижняя части ячеек состоят из двух наклонных стенок.Открытый конец ячейки обычно называют верхом ячейки, а противоположный конец — дном. Ячейки немного наклонены вверх, от 9 до 14 °, к открытым концам.
5. Образец в молекулах —
Кристаллы также построены с математической регулярностью. Химик мог бы легко объяснить, как положительно и отрицательно заряженные ионы натрия и хлорида аккуратно располагаются в кристаллической решетке, в результате чего образуются кристаллы соли с идеальной кубической структурой.А молекулы воды, находящиеся высоко в облаках с температурой намного ниже нуля, аккуратно сливаются, образуя кристаллические снежинки в форме шестигранных звезд или шестиугольных игл.
В кристалле льда молекулы воды расположены слоями гексагональных колец. Эти слои называются базисными плоскостями кристалла, а нормаль к базисной плоскости называется осью c или оптической осью кристалла. Лед — это вода, замороженная до твердого состояния. В зависимости от наличия примесей, таких как частицы почвы или пузырьки воздуха, он может казаться прозрачным или иметь более или менее непрозрачный голубовато-белый цвет.
6. Узор на чехлах Seashell —
Ракушки, поэтому часто украшаются смелыми узорами из полос и точек. Биологи редко задумывались о том, как эти моллюски создают красивый узор, украшающий их кальцинированные дома. Возможно, они просто предположили, что закономерности были точно определены в генетическом плане, содержащемся в ДНК моллюска.
Особым случаем формирования биологического рисунка является появление пигментного рисунка на раковинах моллюсков.Эти узоры очень разнообразны и часто очень красивы. Раковины состоят из кальцинированного материала. Животные могут увеличивать размер своего панциря только за счет нарастания нового материала вдоль краевой зоны, растущего края панциря. У большинства видов пигмент включается во время роста по краю. В этом случае формирование рисунка происходит строго линейно. Второе измерение — это протокол того, что происходит как функция времени по мере роста. Образец оболочки — это, так сказать, пространственно-временной график.Оболочки обеспечивают уникальную ситуацию, поскольку сохраняется полная история высокодинамичного процесса. Это дает возможность расшифровать этот процесс.
7. Образец, обнаруженный в эмбриональном мозге —
Эмбриональный мозг развивается, конкурирующие влияния правого и левого глаза определяют связи, которые устанавливаются в задней части мозга, зрительной коре. Кластеры нейтронов из одного или другого глаза доминируют над частями коры головного мозга в определенном порядке. Считается, что эти закономерности развиваются, потому что нейтроны из каждого глаза конкурируют друг с другом за пространство.Первоначально проекции нейронов, исходящие из левого или правого глаза, немного различаются, и эта разница предположительно возникает случайно. Правила соревнований имеют ту же общую форму, что и правила активации и подавления пигмента шерсти зебры. Проекции нейтронов из одного глаза стимулируют и стимулируют дополнительные проекции в область перед глазом. В то же время эти выступы препятствуют проецированию в эту область другого глаза. Эта местная конкуренция за недвижимость в мозгу приводит к образованию полос, напоминающих полосы зебры.
8. Узор, найденный на песке пустыни —
Самоорганизующиеся модели распространяются и на неживой мир. Они появляются в минеральных отложениях между слоями осадочных пород, на пути удара молнии, когда он падает на землю, в волнистой ряби песка на пустынной дюне. Когда на песчаные дюны действуют силы ветра, гравитации и трения, бесчисленные песчинки рикошетят и падают. Когда одно зерно приземляется, оно влияет на положение других зерен, блокируя ветер или занимая место, где могло приземлиться другое зерно.В зависимости от скорости ветра, размера и формы песчинок этот динамический процесс создает регулярный узор из полос или ряби.
9. Узор, найденный на крыле бабочки —
В небиологических физических системах самоорганизованные узоры являются эпифеноменами, не имеющими адаптивного значения. Не существует движущей силы, которая толкает облачные образования, грязевые трещины, неровности окрашенных поверхностей или спиральные волны в определенных химических реакциях в формирование поразительных узоров, которые они демонстрируют.Однако в биологических системах естественный отбор может способствовать определенным паттернам. Определенные химические вещества в коже развивающейся зебры диффундируют и реагируют таким образом, чтобы постоянно образовывать полосы. Если бы свойства шкуры зебры или состав химических активаторов хоть немного отличались от того, что они есть на самом деле, узор не сложился бы.
10. Узор, найденный в сети Паука —
Паук упаковывает свою липкую сферу в соответствии с генетически определенным рецептом для выкладки различных радиусов и спиралей паутины.Личинка ручейника строит замысловатое убежище из песчинок или другого мусора, тщательно скрепленных шелком. Другой очень распространенный пример вызванной организации — соты, сделанные пчелами (рис. 5). В таких случаях в строительстве зданий действительно участвует маленький архитектор, который наблюдает и устанавливает порядок и закономерности. Нет никаких «субъединиц», которые взаимодействуют друг с другом для создания паттерна; вместо этого каждое из животных действует как каменщик, измеряя, устанавливая и перемещая части на место.

 Так повторите ещё три раза.
Так повторите ещё три раза.